原文 自动优化出的通用的pattern, 以及通用的decoder。
目标
结构光可以非常准,但那需要很多的patterns投影,而减小patterns的数量会造成结构光不稳定、不鲁棒,产生噪声。由于真实环境场景条件的复杂性,在某些条件下有效的pattern design 和 decoding 方法,换种条件可能就无法达到最优或者干脆失效。这里的条件包括外部条件:间接光照(环境光),低照度环境(低PSNR),物体的材质,相机传感器的噪声等;也包括人为可控制的结构光条件:pattern数量、pattern频率的上限、感兴趣的深度区域范围或者bounding box等。
很多的研究中,需要对这些条件做各种假设和前提,来针对性地设计确定好的pattern和相应的decoder,但这篇文章希望将这个过程自动化,用一个足够通用的方法,给出结构光的设置条件,就能得到一个对大部分场景条件都能起效的pattern,并且得到一个较为通用的decoder。
这篇文章不对以下条件做假设,换句话说,它希望得到的pattern能在这些条件中通用:
- 间接光照和环境光
- 噪声,包括由照度不足、硬件限制等造成的各种成像噪声
- 被测物体的材质和具体摆放
- 投影仪的工作状态,(可能出现defocus没完全对上焦等)
本文将根据以下控制条件优化出pattern:
- pattern数量
- 最大频率
- 对像素匹配误差的容忍度
a la carte是法语,意思是“点菜”,也许菜单是pattern,而你给出的条件就是budget吧。
可优化结构光的框架流程
采用temporal的序列pattern,流程很简单(投影-拍照-匹配-算深度):
- 依次投影出pattern
- 每次都由相机拍一张照
- 多张找的每个像素形成一个 code array
- 将每个像素的code与多个pattern合成的code matrix里的每列匹配
- 匹配成功后,根据相机和投影仪的内外参,三角测量求深度。
我希望它能根据给出的pattern数量、最大频率F和误差容忍度等自动调整优化出最合适的Pattern,那就需要有一种反馈机制,forward-loss-backward那样。 结构光的偏差显然是最终的深度的偏差,而深度直接来自且只来自视差(不考虑相机和投影仪参数等),也就是在像素的code array和pattern的每一列的code之间的匹配。loss的来源是这个匹配。
那么,优化的流程就是:
- 依次投影出待优化的pattern
- 每次都由相机拍一张照
- 多张找的每个像素形成一个 code array
- 将每个像素的code与多个pattern合成的code matrix里的每列匹配
- 评估这个匹配的结果,形成loss,然后反向传播优化pattern
接下来的问题就是,如何设计loss,以及如何让这整个流程可微,从而能够反向传播?
重要的数学符号:
| 符号 | 解释 |
|---|---|
| K个pattern | |
| pattern一行的像素数 | |
| 相机照片一行的像素数(W) | |
| Code Matrix | 每一列表示一个code |
| Observation | 投影K个pattern后拍照得到K个H*W的图片,将它们stack起来形成新的dim=-1,最后那个维度就是这个像素的 code。后续处理中一般不会考虑H,只考虑一行,因此它简化成了一个矩阵。 |
对结构光流程的建模
需要对结构光重建的流程建立全部可微的数学模型,自己可以设计的主要就是三个过程:投影、拍照成像和匹配(或decode)。
并不从物理角度进行建模,下面的模型都是 plausible,“看着像就行”的。
投影建模
这个一般不建模。就把投影仪当做是反向的相机,用于投影的pattern是什么样,投影出来的光就当做是什么样。不过这里给出了个可选的模型:考虑投影仪的defocus。所谓defocus就像是相机没对上焦,物体没在景深范围内,一个实像点投影到了传感器的多个像素上,投影仪的defocus也是如此,场景中某个点接收到的投影仪光线来自pattern的多个像素(跨越了多列),如下图。
这个模型很简单:场景中一个点收到了来自投影pattern中多个列的贡献,可以直接用贡献权重建模。同时,直接在图片坐标中建模更方便。这是一个 shape 为 (M, N, N) 的张量 ,在图片的m列(所对应的场景中点)处,第 n0 列的 code 会与 N 个code因defocus发生混合,其中第 n1 列code的对这第 n0 列 code 的混合贡献权重是 。因此考虑 defocus时,要先利用这个 对code matrix 进行预处理,加上 defocus效果。
实现中它也不是真的要从物理角度去测量这个张量 ,首先忽略 相机图片不同列(M那个维度)的效果差异,即实现中 B 沿着第0维是一样的,那么B就是个矩阵。而对code matrix的每列而言,defocus带来的混合直接建模为每一列code与它左右相邻的若干列的均匀混合,这就很简单了:
这样,考虑defocus的时候,直接将 C, B 矩阵相乘即可。如果不考虑 defocus,B相当于一个单位矩阵。
成像
成像的建模尤其是 Plausible 的,所以不要过多从物理的角度去考虑。首先大幅简化:假设相机图片的一列code array 来自且仅来自于 code matrix 中的一列。这个过程可以用一个传播矩阵 来描述,只考虑图片中的一行像素的code arrays 形成的矩阵 ,,那么 T[p, q] 表示 code matrix 第 p 列 对观测结果图片的 第 q 列 code array 的贡献权重。由于前面的唯一来源假设,矩阵 T 的每一列只有一个元素不为0。
此外,再考虑环境光和噪声因素。噪声可以用各种方法建模,比如最简单的正态分布,或者其它任何噪声模型。
对成像过程的建模也很简单: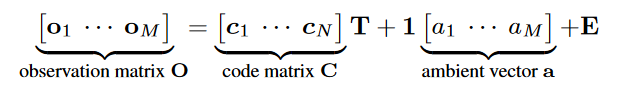
注意O 的一列是同一个像素在不同位置下的像素值,既然是同一个像素,那么它所接受的环境光也相同,所以环境光相当于只是一个长度为 M 的向量,广播出新的长度为K的第 0 维。
T有个重要的性质,由于前面的唯一来源假设,它的每列只有一个元素非0. 假设投影仪在相机左边,而投影仪和相机有相同的内参、pattern和照片的宽度也相同,那么 T 就是方阵,且是下三角阵,非0元素只在主对角线下方。进一步可以考虑添加几何约束:即我人为限定场景中物体的深度范围,或者左右范围,这样匹配点的约束进一步增强,T中元素可能非0的区域也就越来越小,如下图。从之后可以看出,加了这些约束后,方法能更“专注”优化那些可能被用上的codes,从而表现地更好。

decode与匹配
这篇文章证明了ZNCC是对各种code matrix通用的解码器,因为:
在噪声标准差趋近于0、code matrix各列的方差的方差趋近于0的时候,不论采用何种code matrix设计,寻找“使得拍出观测 概率最大的匹配code ”的结果趋近于寻找令 ZNCC 最大的 列。
证明在这篇文章的支撑材料中,很长没看()
好的,确定使用 ZNCC 作为相似度度量,那么接下来如何让 argmax 这个东西可微,或者如何利用ZNCC 来设计损失函数?目标是让 与 真正匹配的 与 的ZNCC尽量大,而其它 与 的ZNCC 尽量小,找个越是满足这条,就能让结果越大的算式: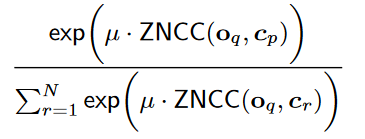
越大,越能体现分子要大、而分母中除了分子以外的都要小。文中取了 。嗯, 的数量级是 1e130。
这个数越接近1,就说明结果越符合我们的预期,越能通过 argmax 的匹配得到正确的结果。此外,这个式子要求必须100%匹配正确才能算对(分子只有一个),我们可以引入误差容忍度 ,允许匹配结果差上一点也算对,进而: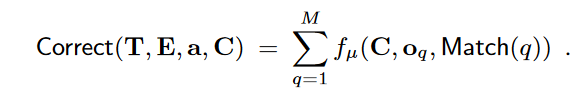
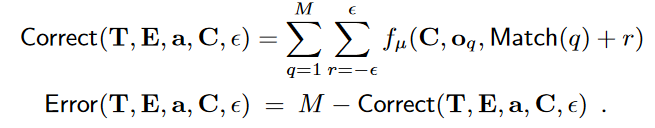
第一行将观测的一行的所有像素的correct相加,第二行引入 容忍度,在算每个像素的 correct 的时候允许偏差一点也算对,第三行总量减correct得到 error。
最后,注意,我们希望模型优化的结果对于大部分场景条件(环境光、噪声、物体位置等)都有较好效果,所以最终的损失函数(也就是优化目标)是个期望: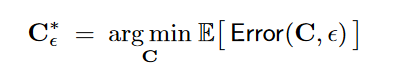
这里的环境条件其实就是 T(代表了场景物体信息),环境光ambient,和噪声 E。
期望当然是用多次采样求平均去近似,损失函数: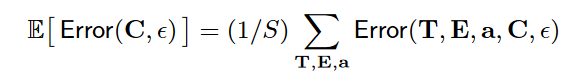
优化算法
有了上面的各个环节的建模,算法其实就出来了。
randomly initialize the code matrix C
while not converged:
T, A, E = sample_conditions(n_samples)
obs = compute_observation(C, T, A, E)
err = compiute_error(C, obs)
err.backward() 另一个角度
抛开这些成像、匹配等过程的建模,但从优化算法数学公式来看,这个方法其实就是在code matrix空间中直接优化code matrix的每列,观测 的每一列就是“选出code matrix 中的某一列”针对性“优化。传播矩阵 就是随机选出一些要针对性优化的列,ambient 和 noise 加上扰动:前者是bias,后者有点像是variance。然后,correct(即error函数)衡量这列被选出来的code(经过随机扰动后)与所有code的相似度,然后反向传播让这个相似度最小。
整个算法就是依次针对中的每列,让它与其他列的ZNCC相似度最小。所以考虑 geometry constraints 后效果明显更好,因为它限制了T中非0元素可能存在的范围,能够只针对可能被用到的codes做优化。
限制最大频率
从后面的实验可以看出,限制pattern的最大频率对于最终的重建结果非常重要,这就好像是某种 regularization。做法也很简单:迭代完一轮后,先将 C clip到[0,1],在离散傅里叶变换DFT,将频率大于max frequency 的部分的系数直接置0,然后逆向傅里叶变换,clip到[0,1],之后才进行下一轮迭代。
实验
| 硬件 | 使用blender模拟,未加参数。相机和投影仪根据blender的设定计算理想内外参。分辨率均 |
|---|---|
| 代码 | 这里 |
| 备注 | 未考虑几何范围约束,未考虑投影仪defocus。虽然有所实现,但不完全或没测试。=300,迭代1000轮。提前采样250组条件<T, A ,E>用于evaluation |
| 场景 | groundtruth depth |
|---|---|
 | 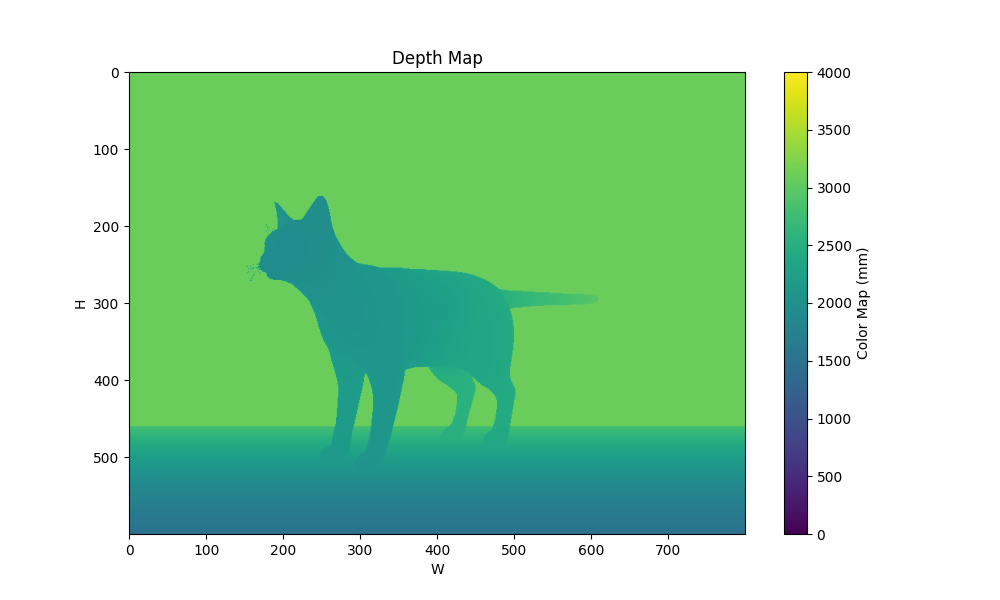 |
| 条件 | code matrix | 相似度矩阵 | 深度图 |
|---|---|---|---|
| patterns 4 maxfreq 4 0 |  |  | 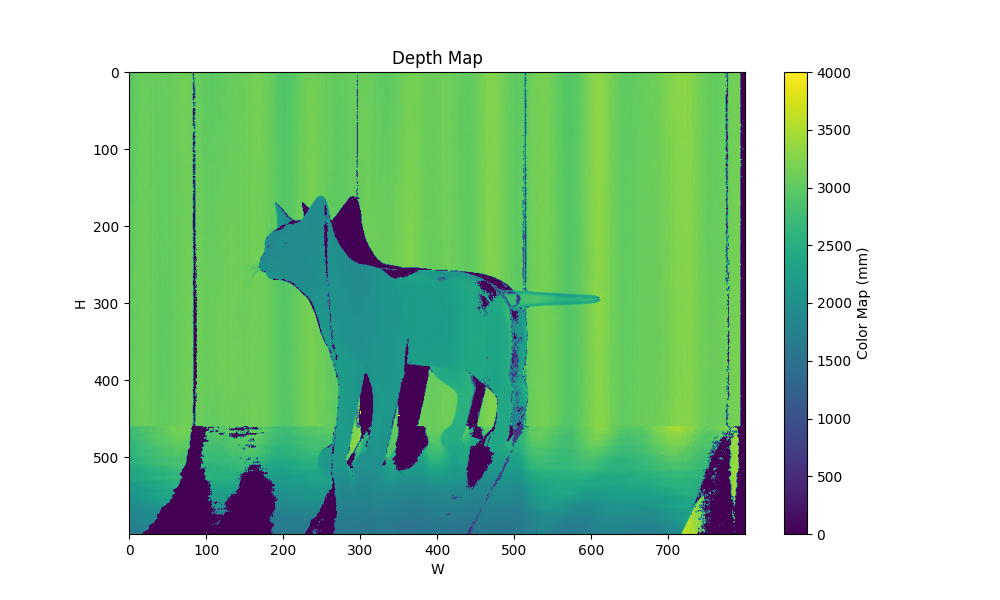 |
| patterns 4 maxfreq 4 3 |  | 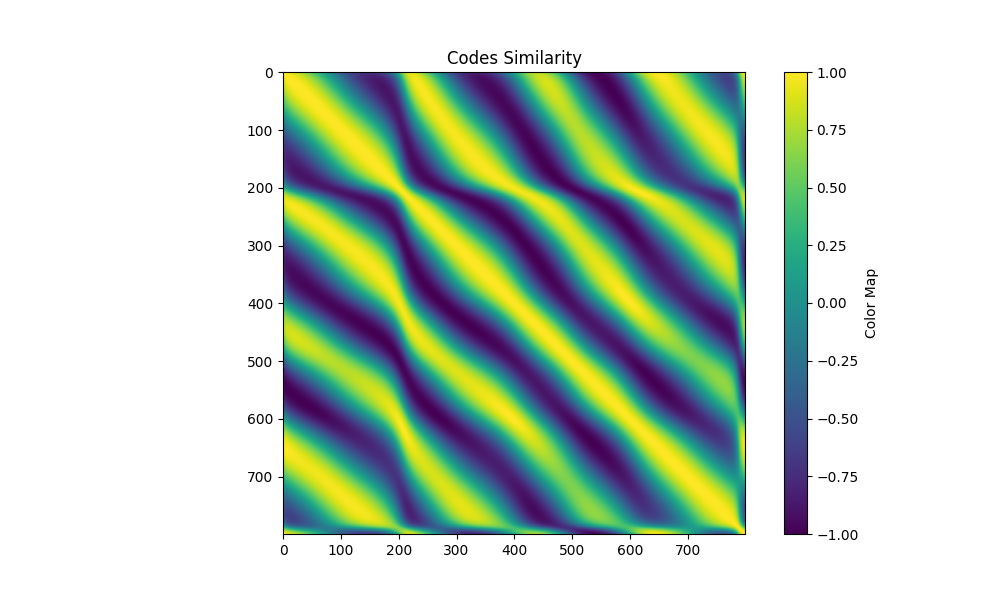 | 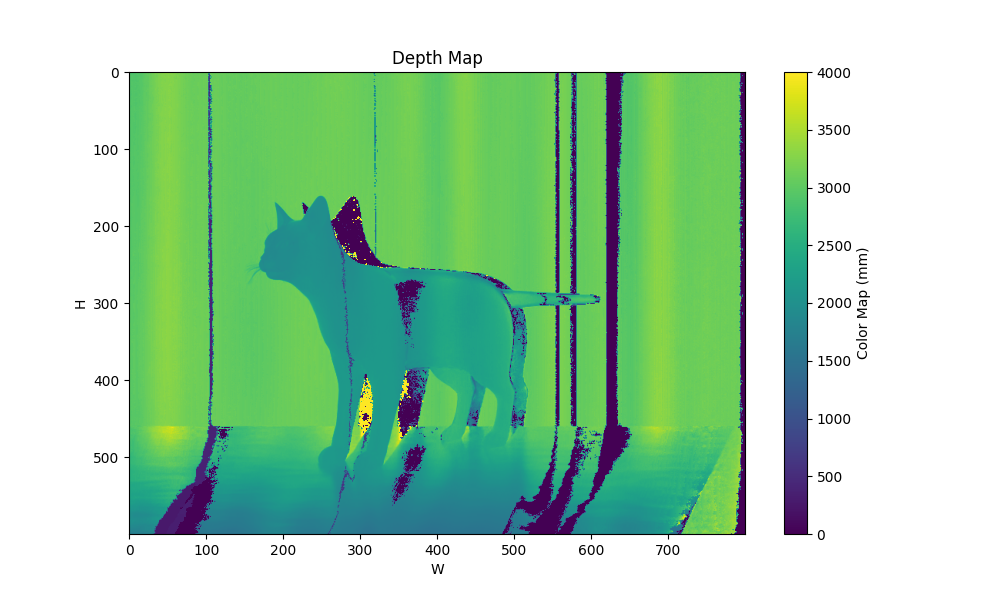 |
| patterns 4 maxfreq 8 0 |  | 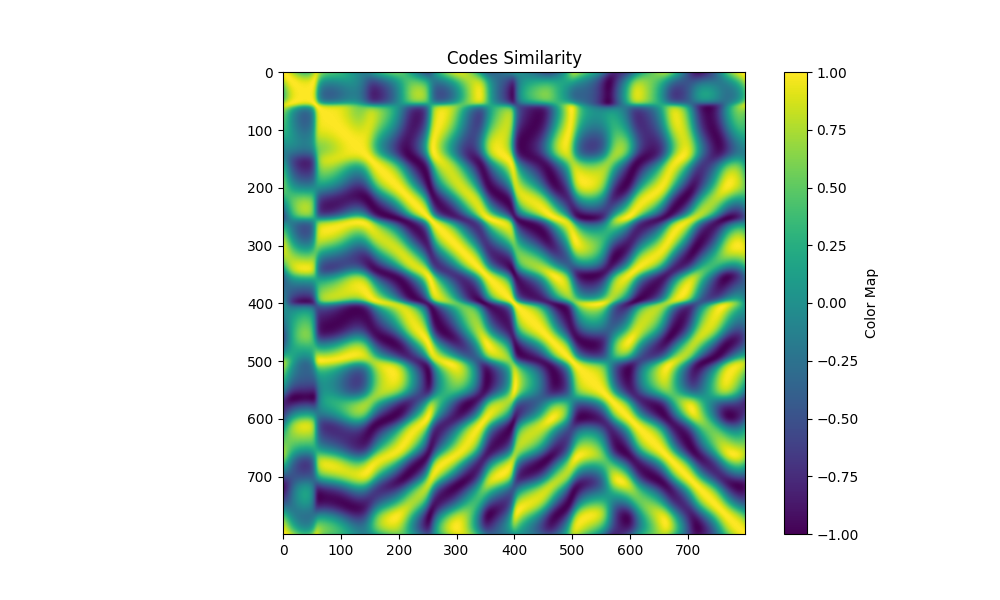 | 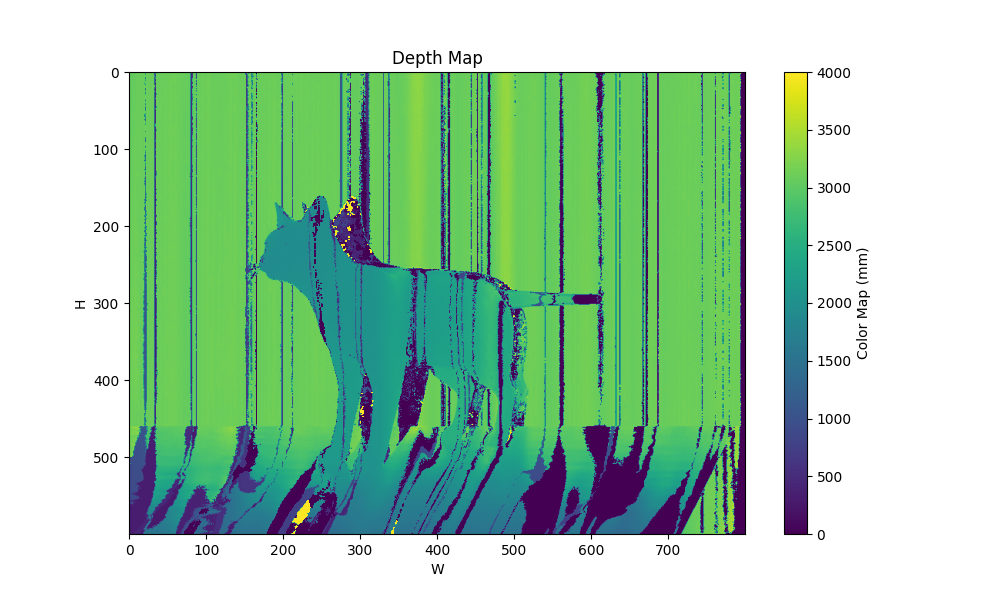 |
| patterns 4 maxfreq 8 3 |  | 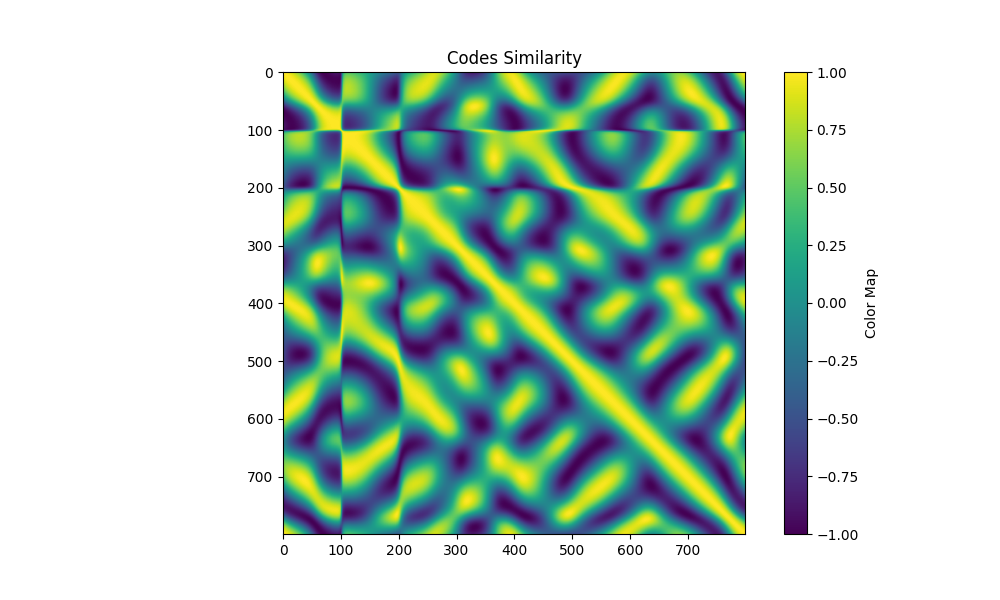 | 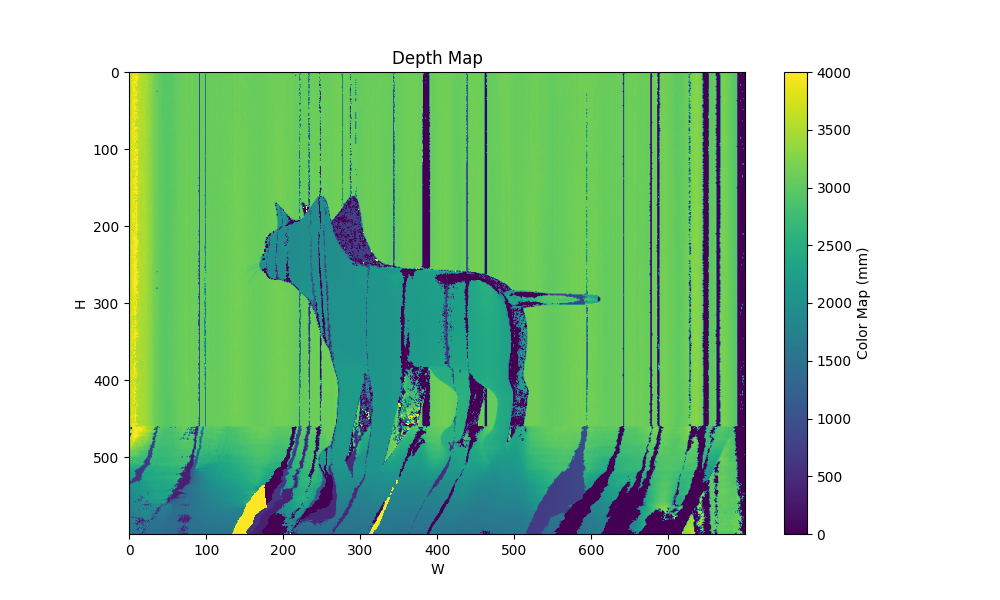 |
| patterns 4 maxfreq 16 0 |  |  | 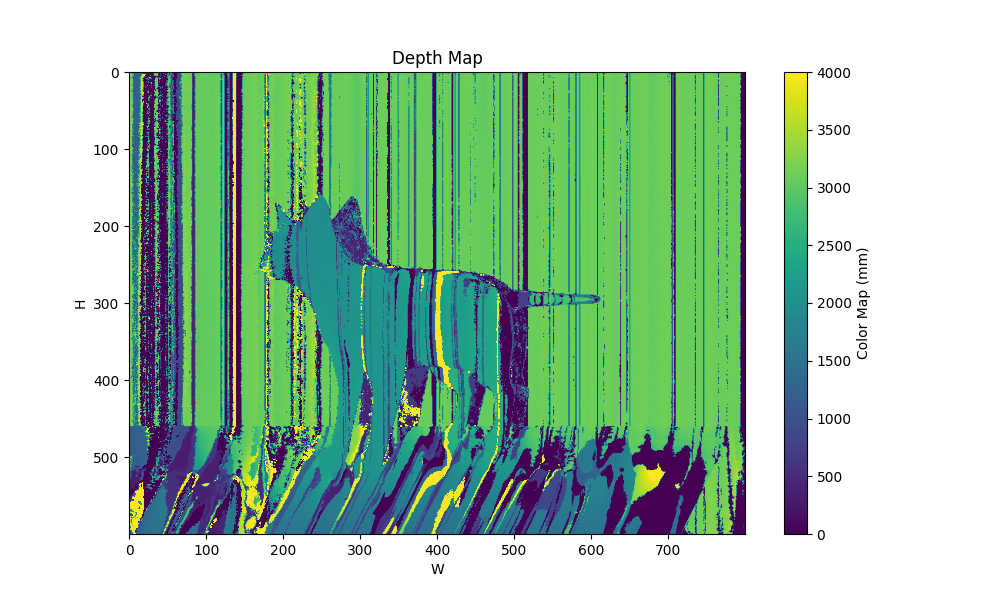 |
| patterns 4 maxfreq 16 3 |  | 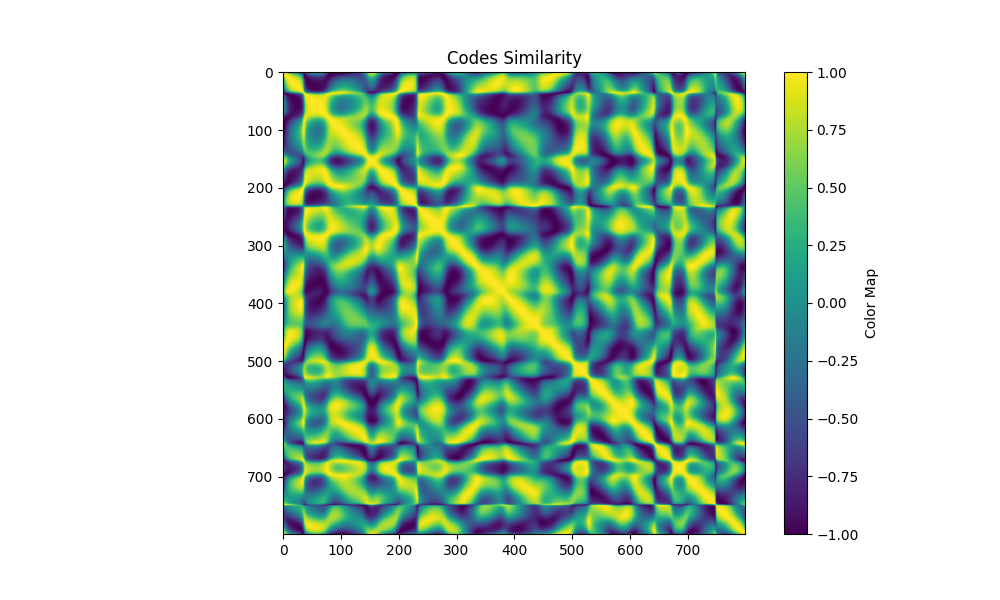 | 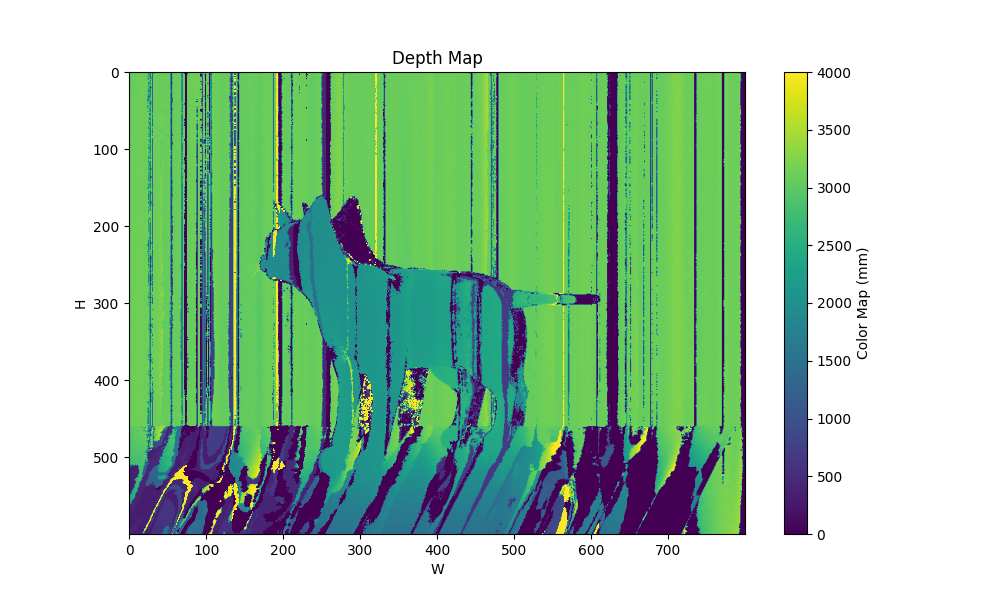 |
| patterns 4 maxfreq 0 |  | 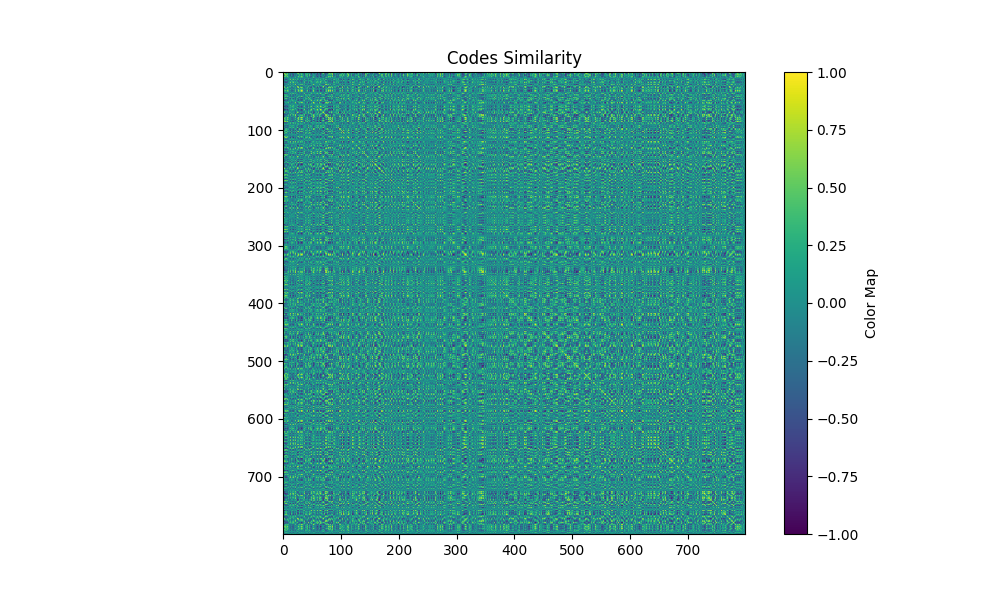 |  |
| patterns 5 maxfreq 4 0 |  | 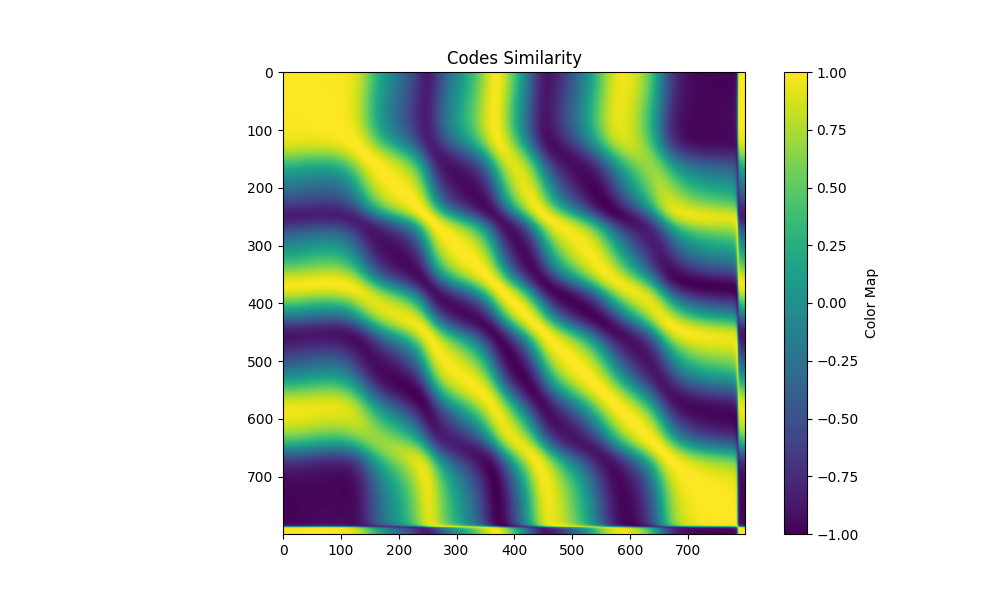 | 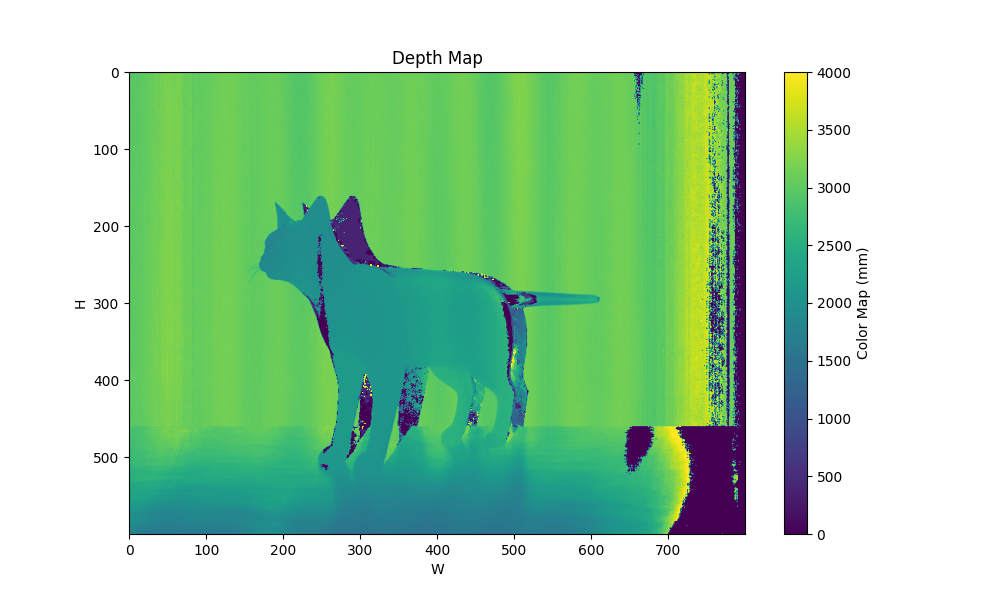 |
| sinshift freq=4 shifts=4 |  | 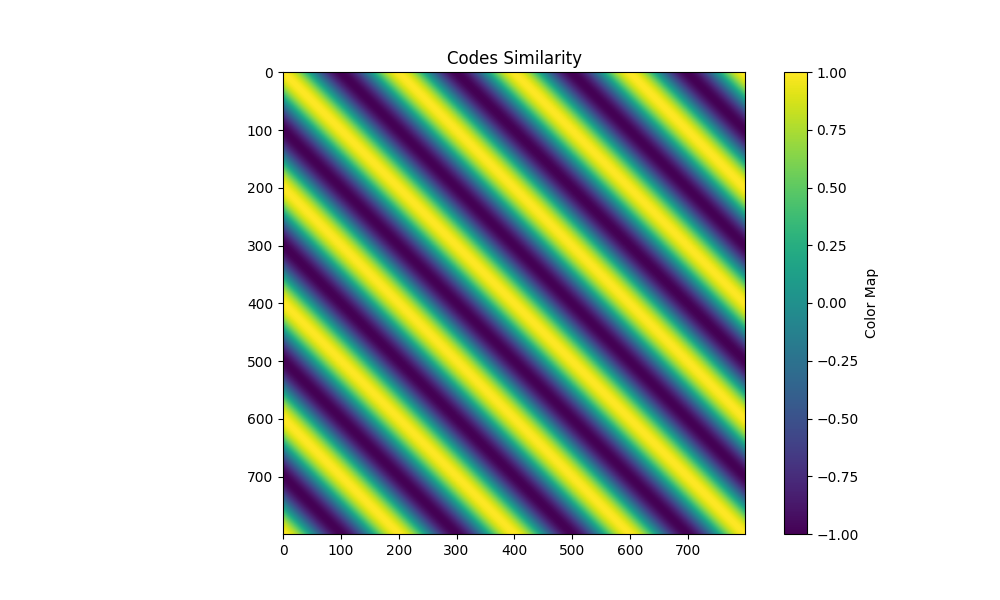 | 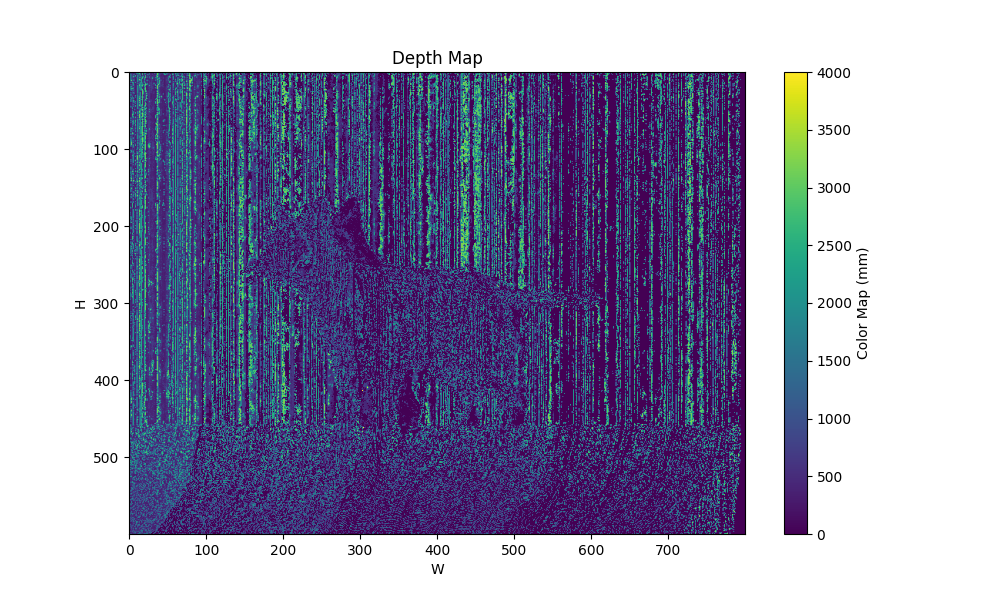 |
踩坑
代码量不多,但写bug快debug难( 。 此处记录一些印象深刻的。
张量索引
张量计算实现该算法涉及到不少索引,我自己对pytorch不太,…,:,高级索引用的不利落,混在一起同时用更是如此。所以会有能运行但结果不对的情况——索引错了。最后复杂的索引都用了高级索引不太简洁的做了。
浮点数
这篇文章的方法比较特殊,数值来到了 也就是 1e130 的数量级,需要用双精度浮点数 double。图省事直接设置了default dtype,这导致显存翻倍,所以只存了250组条件用于eval。此外还有浮点数精度问题,浮点数计算操作数的数量级不要差太远。
ZNCC的实现
这个问题的发现来自于,不限制最大频率的时候训练没有问题,但限制最大频率后突然无法训练了:code matrix从一开始就固定在几乎全是0.5的数据,此后不变了。我很快发现这是因为随机化的数组虽然看起来很杂乱,但频率很低,DFT后几乎只有第一个参数(频率0)较大,其它的都非常小,因而限制最大频率滤掉高频分量后,剩下的几乎只有频率0的分量,所以逆变换回去数组各元素的值几乎一样。我一开始下意识觉得无法训练是因为梯度下降更新的变化无法“突破”限制最大频率后滤波掉高频分量的“阻力”,于是我最开始尝试用初始化的方法先跳出全是0频率的坑。——但是没用,即使我直接在频域随机化,然后再将其逆变换回去作为初始值,都无法逃离最终变成几乎全是0.5的code matrix的结局。
直到我在不限制最大频率的条件下,尝试训练一个初始化为全0.5的code matrix,报错了nan,这才发现是ZNCC的锅。
如果code matrix的每一行都非常相近,那么将这一行减掉它的平均值,每个元素就会变得很接近0,由于之后涉及出发,这会带来数值计算的问题。
解决方法是在ZNCC的分子(注意不是分母!考虑两个每个元素都相等的数组的ZNCC)里加上一个小数,比如 1e-6.
然后就可以训练了,很神奇。
最大频率的影响
从最后效果来看,限制最大频率非常重要,只看可视化图的情况下,几基本上最大频率越大则可视化图中的异常点越多,原文支撑材料里的图也是如此: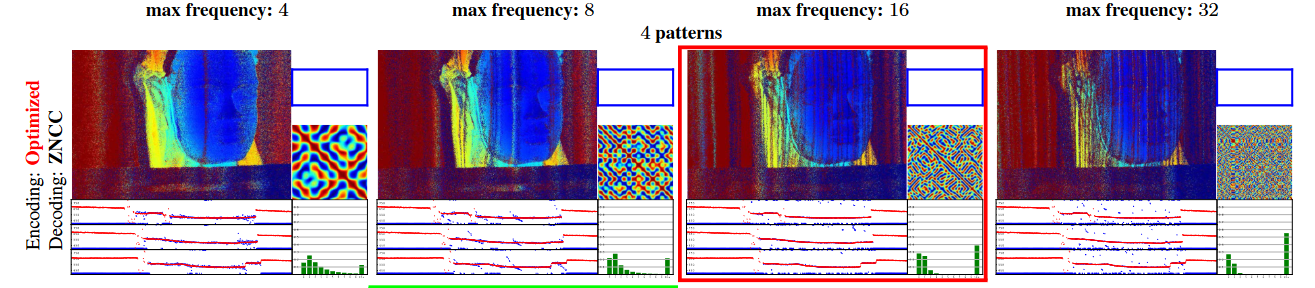
我的结果里也有这样的趋向,尤其是不限制最大频率的时候,即使损失函数值能降到比较小,但实际使用得到的深度图很差。不限制最大频率得到的Pattern有点像”充分利用每一个灰度级“来形成pattern的意思,太容易受场景条件干扰而失效。
但这也不代表频率越高越坏,低频导致相邻列的code必定相近,虽然最终可视化整体效果好,但可能不乏错误匹配到了相近列的情况,但深度差异较小所以颜色差异也小,看起来就好;高频pattern可能虽然有更多匹配飞了,但匹配上的部分准,有点像钝(平滑)和锐的感觉…我没具体分析数值上的差异。
关于损失函数值
关于损失函数值的优化,可能是我的实现或者参数设置还有点问题,虽然能够优化、数值能够下降、得到的pattern效果看起来也不错,但损失函数值挺大的,下降幅度也很小,尤其是最高频率较低、容忍度小的情况下。
感觉其实也比较合理,correct是 ,所以越多和matched code相似的越多这个correct就越小。限制了最大频率后,相近的几列大概率会比较相似,而哪怕只有10个比较相似的code,correct都只有1/10了,每列都有这样比较相似的,总的算下来error就大了。但error数值大,最后优化出来的Pattern效果应该还是可以的。
提高最大频率,提高容忍度,就能降低error数值。
也可能是我的实现还是有点小问题,或者参数设置不对,比如我给的随机环境光、噪声的影响都挺小的。

