结构光（一）简单基础

Overview#

结构光的本质就是双目视觉，结构光重建也完全基于双目相机的重建，也就是三角测量。而传统双目相机的重建流程，大致是：

相机标定：内外参（小孔相机模型）
极线矫正（不必须）
像素匹配
三角测量算深度

最后的三角测量是最简单的，只需要根据给定的内外参和匹配的像素点，解三角形即可。
标定和极线矫正都是比较老的算法，有大量研究花在了像素匹配这个问题上：如何知道两个相机中的某对像素，来自于同一个空间点？这必须要图像像素之间存在能够被比较匹配的差异，也就是存在特征，也就出现了各种特征的设计，比如广泛使用的SIFT等。
但是在计算深度图的时候，我希望尽量让所有的像素都能找到自己的匹配像素，那么这些特征就可能捉襟见肘了：比如，面对一面没有纹理的白墙，任何特征匹配都将失效。

没有可供匹配的特征——那我就创造特征不就行了？将一个相机换成投影仪，往场景中投影可供对比匹配的特征图案（pattern），让另一个相机拍照，然后将相机拍的照片和投影仪的特征pattern进行匹配。由于投影仪可以看做是将光路逆转过来的相机，投影仪+相机的系统完全可以看做是双目相机系统，可以在投影仪pattern和相机拍摄的图片之间做三角测量重建。

那么，问题主要就是：如何设计最容易被识别匹配成功的pattern（encoding），如何设计相应的识别算法在pattern和照片见找到对应点（decoding），然后让这些方法在复杂的现实场景中能够起效。

小孔相机模型#

这个不太想写什么了，浅显易懂，主要就是几个坐标系的变换：屏幕坐标系（像素为单位） —— 成像平面坐标系（实际距离单位）——相机坐标系——世界坐标系。其中，世界坐标系-相机坐标系的变换是外参，后面的是内参。
这几个变换都是挺简单的相似三角形，不过写成矩阵形式。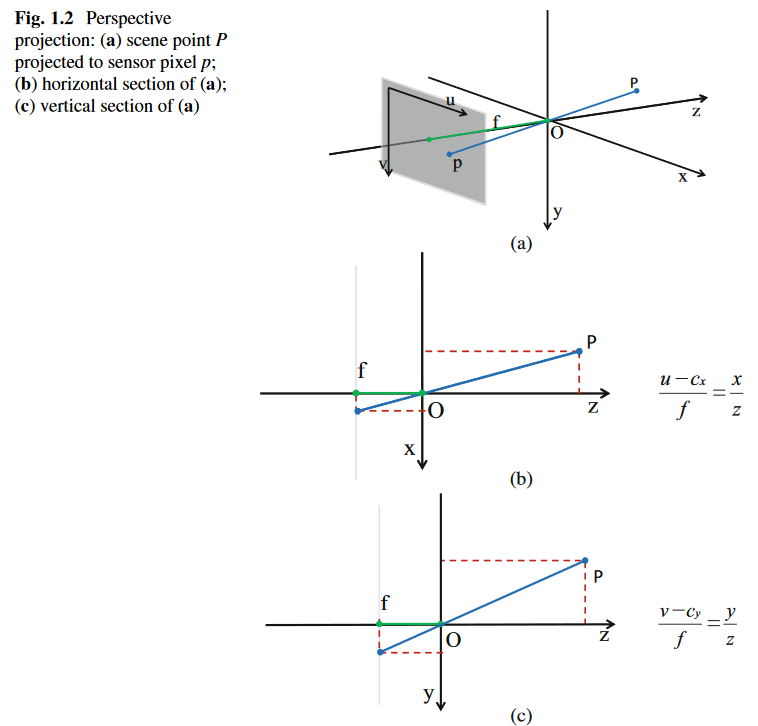
小孔相机坐标变换

假设相机坐标系下空间点坐标（x,y,z），成像平面坐标系（u,v），则这一步投影关系可以很简单地写成矩阵形式：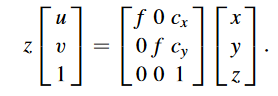
相机坐标系-成像平面

从成像平面坐标系变成像素坐标也很简单，uv乘以横纵轴像素密度（像素/单位长度）即可。
从相机坐标系变成像素坐标系的矩阵称为内参，而从世界坐标系变换为相机坐标系的矩阵称为外参，外参反应了相机的位姿。

NOTE
严格来说，由于相机的各种误差，相机坐标的x,y可能不被视为垂直，所以在内参矩阵K的第一行第二列放多一个变量 $\alpha$ 。一般忽略。

假设世界坐标系下的空间点坐标 $P_W$ ，相机坐标系下的空间点坐标 $P$ ，两者之间的变换就是相机相对于世界坐标的旋转与平移：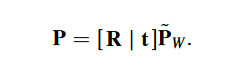
外参矩阵
$\~P_W$ 是齐次坐标。

合到一起：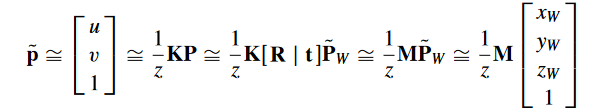
小孔相机模型总变换

$\~P$ 是成像平面坐标系下的坐标。
总的变换矩阵 M：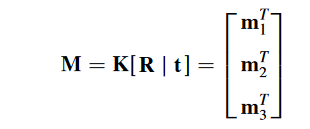
变换矩阵M

求解M#

求解 M 就是标定所做的事。假设已知若干对个 <像素坐标，空间点坐标>（暂且记录为 $<p^j,P^j>$ ）的点对数据，对于每个配对数据，可以列两个方程：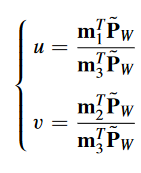

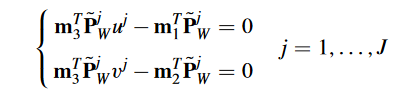
而3*4矩阵M有12个未知数，所以需要12个方程，6个点对即可。但自然一般会用很多冗余。

这样的做法叫做直接线性变换（DLT），只能“minimizes a target with algebraic significance, and is not invariant with respect to Euclidean transformations.”（没明白，但就是有缺陷），一般会拿这个结果作为初始值，然后用其它更高级点的优化目标或方法，比如用最小二乘：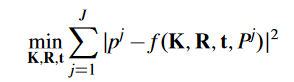

KRt就是内外参，也就是M。

相机畸变#

光学系统的畸变情况很多，算法中一般不考虑太多，直接当做是distortion $\psi$ ：它把原本应该位于 (u, v) 的像素，ditort到另一个位置 (u’,v’)。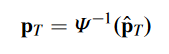
相机畸变distortion

一般直接用多项式去拟合这个变换：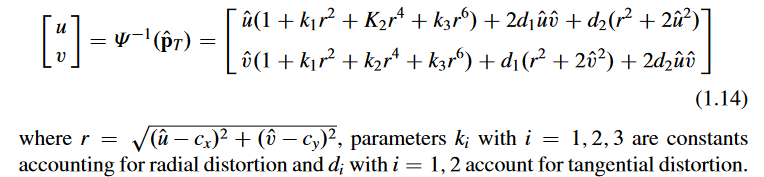
多项式拟合distort

畸变参数 $d=\{k_1,k_2,k_3,d_1,d_2\}$ 。
因此，要标定的参数集合变成了 $\{K,R,t,d\}$

相机标定#

就是拟合上面的参数集合 $\{K,R,t,d\}$ 。没看具体怎么做。

极线矫正#

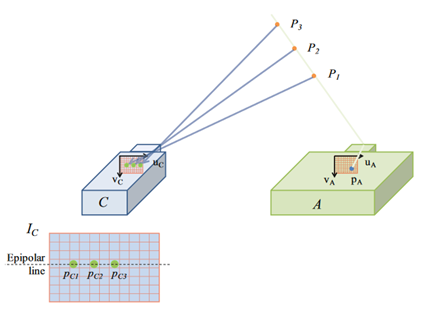
当两个相机对齐（rectified）的时候，有一个很好的几何性质：

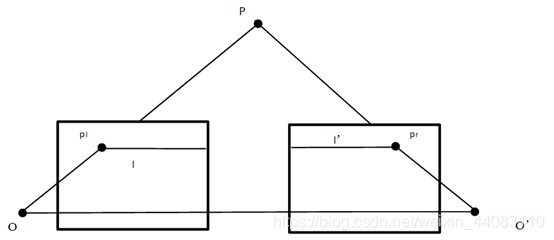
极线矫正（对齐）

将相机A的小孔、虚线面上的像素和相机B的小孔形成的三角形的平面扩展，会交两个虚像面于两条平行线，这个像素所可能的对应点就在对方虚线面的这条线上。对于对齐的两个相机来说，就是一个像素在另一个相机上的对应点，一定于它水平（在同一行）。因此，这就把匹配点从二维搜索降到了一维搜索。

若是没有对齐，这个结论页成立，不过不是水平线而是斜线了，这和相机之间的相对位姿有关。

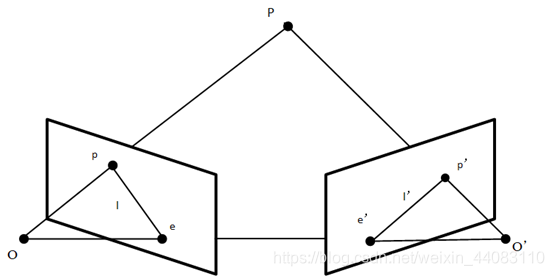
极线（不对齐）

结构光系统同样也适用这一点，一般会让投影仪和相机对齐，这样只用在水平线上进行匹配搜索，让投影仪的pattern只用在水平方向上有区别即可。

投影仪-相机系统的极线

具体怎么极线矫正（其实是对齐rectify），我没看（）。

关键点匹配#

没看。双目视觉中的关键点匹配可以很复杂，但结构光因为人为投影pattern，匹配方法一般比较简单。
简单：比如，就是遍历可能的像素去计算相似度，选最大相似度的，而这个相似度一般也非常简单，譬如在相邻像素组成的窗口内逐像素求差求平均（当然，比较古老）…

结构光投影Pattern的设计#

结构光是为了给不易匹配的场景投影加上易匹配的pattern，核心问题之一就是如何设计pattern。一般来说，pattern的设计有四种自由度：wavelength (channel), range (pixel level), temporal, spatial。

衡量pattern的方法就是要uniqueness，一种方便的可视化是让pattern的列之间两两计算相似度形成相似度矩阵。一种比较理论的方法是，在实际使用的时候，让实际照片和pattern匹配的同时，找到相似度次大的那个code与这个像素的相似度（因为匹配的时候会匹配到相似度最大的那个code），如果这个次大的相似度与最大相似度差别大，uniqueness就强。

directed pattern#

直接的结构光pattern就是最直接的pattern：给每个像素赋予不同的颜色或灰度值。但是这会显著地受环境和设备因素影响，很不稳定，一般不单独使用。

temporal pattern#

这是最准的方法。如下图所示，依次投影K个pattern，这样每个像素在K各pattern上接受到的灰度值（或颜色值）形成了一个长度为 K 的数组，temporal pattern 让同一行的各个像素的这个特征数组各不相同。

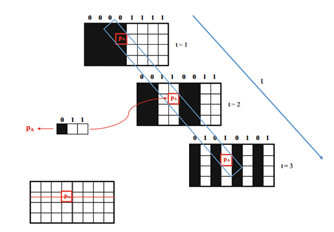
temporal pattern

我们将一行中每个像素在K patterns中收到的特征数组排列成矩阵，就形成了编码code。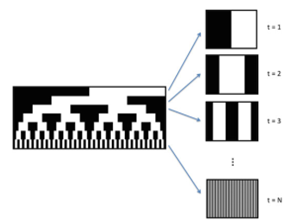
temporal sl encoding

比如这个图就是7个Pattern形成的。每一行提出来，上下填充repeat，就能形成7个pattern。

基于格雷编码#

基于格雷码的方法是最经典的0-1 temporal pattern的设计，让最终的code matrix的每列之间构成格雷码。

Phase shift sin/cos#

通过不断堆砌pattern的数量，结构光可以达到非常高的精度（比如，每个patter只让所有列中的一列为白，其它全黑，然后投影width个这样的pattern）。

用正弦函数+相位偏移也可以做类似的事，用正弦或余弦函数来形成每列的code，一般有这几个控制条件：正弦函数的周期数（频率）和相位偏移数量，最后形成 n_freq * n_phase_shifts 个pattern。

每个pattern的公式为：

I(x)=I_0(1 + \sin(\frac{2\pi f x}{P}+\phi))

其中， $I_0$ 是标准化函数，将结果缩放到[0,1]，f是频率， $\phi$ 是相位偏移（指定n次相位偏移，每次偏移相位 $\frac{2\pi}{n}$ ），常数P和变量 f 决定了在同 $\phi$ 情况下的相位的步进，可以设为1。

下面的代码展示了频率1~16，相位偏移10次形成的patterns（一共160个）。

import numpy as np  
import matplotlib.pyplot as plt  
  
# 图案参数  
width = 800  # 图像宽度  
height = 600  # 图像高度  
frequencies = np.arange(1, 17)  # 频率从1到16  
phase_shifts = np.linspace(0, 2 * np.pi, 10, endpoint=False)  # 10次相位移动  
  
# 生成图案  
patterns = []  
for freq in frequencies:  
    for phase in phase_shifts:  
        x = np.linspace(0, 2 * np.pi * freq, width)  
        y = (1 + np.cos(x + phase)) / 2  # 正弦波图案  
        pattern = np.tile(y, (height, 1))  # 重复图案  
        patterns.append(pattern)  
  
# 显示图案示例  
fig, axes = plt.subplots(16, 10, figsize=(20, 32))  
for i in range(16):  
    for j in range(10):  
        axes[i, j].imshow(patterns[i * 10 + j], cmap='gray')  
        axes[i, j].axis('off')  
plt.show()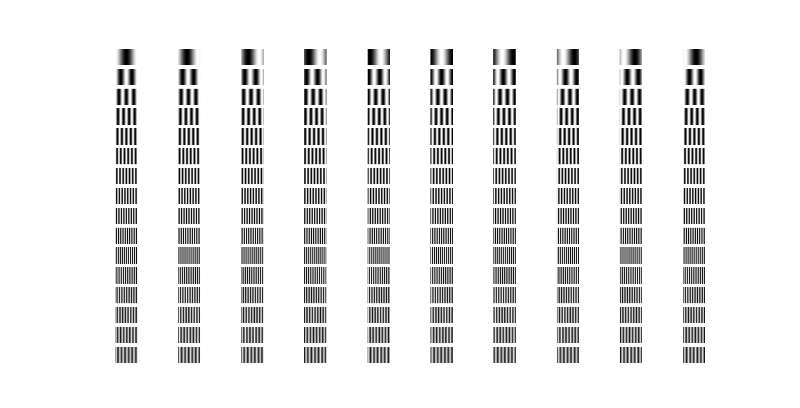

160 phase shift pattern result

Spatial pattern#

temporal patterns可以达到很高的精度，但速度较慢。Spatial pattern试图只用一个pattern。直接pattern尝试直接让每个像素都不同的做法不太可靠，但让某个固定大小的滑动窗口内的像素群unique是很有可能，也更为鲁棒的。spatial pattern做的就是这个：让一个固定大小的滑动窗口内的pattern独立。

大部分消费级实时深度相机都是用 spatial pattern。

将Pattern可能用到的值视作一个字符集，只考虑极线，一行pattern像素就是一个字符串，spatial pattern的任务就是让这个字符串的任意长度为 t 的子串互不相同。

有多种方法做到这一点，比较有代表性的就是 de brujin 图。这个图的介绍建议看维基百科。首先，给定一个字符集B以及字符串长度 t，这个字符集可以排列出 $P_{|B|}^t$ 种互不相同的长度为t的字符串，这些字符串就是 de brujin 图的顶点。图的边这样形成：如果字符串 a 可以用字符串b 通过这种方式构造：将 b 的各个元素向左移动一位（最左边的丢弃），然后在最右侧补充一个字符，那么就构建边 <b, a> （b->a.）。这个图有很多条回路（定量忘了），并且每个回路都是哈密顿回路，而且每个回路的节点（长度为t的字符串）互不相同，并且相邻节点的字符串能够首尾拼接。顺着这些回路走完一圈，就能形成满足前面条件的 pattern 的一行。

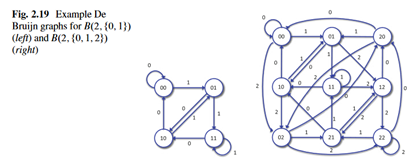
de brujin graph

可见，B就是所有可能采用的像素值的几何（比如0-1），而 t 就是所设定的滑动窗口的大小。

由于 de brujin 图有很多个哈密顿回路，所以用它形成的spatial pattern可以让每行之间都不一样，从而不再强烈地要求极线矫正。

当然，spatial pattern还有其他很多设计。