图神经网络·GCN, GraphSAGE, GAT

图神经网络GNN是处理图数据的网络，而不是网络本身的结构是个图。网上搜索GNN一般会直接蹦出来关于清华孙茂松组在2018年的一篇关于GNN的综述：Graph Neural Networks: A Review of Methods and Applications。

综述里对GNN的分类是这样的：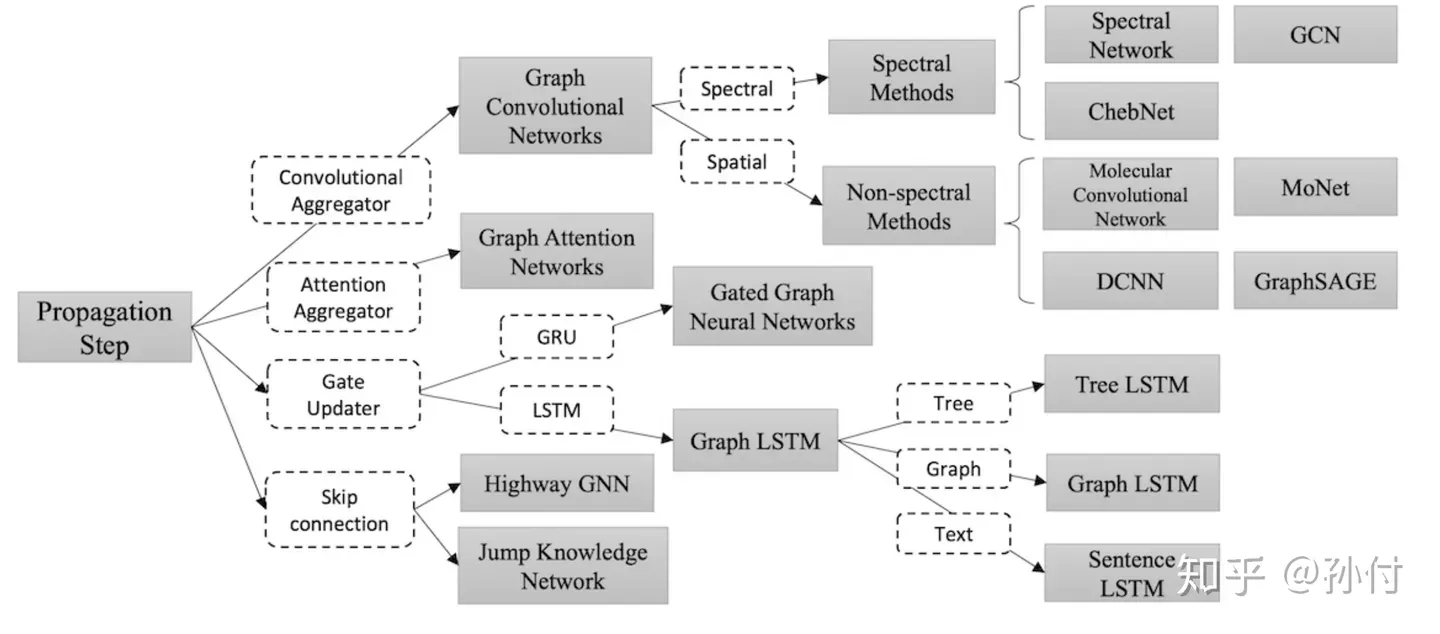
GNN分类

关于这个综述，(为了省事…)我主要看的是这个综述简介，里面涉及了一些GNN的公式的简单而不求甚解的讲解。

GNN的任务#

GNN的任务本质是编码。输入一个图，图有节点V、有边E，每个节点和边都有自己的特征x，GNN的任务就是对每个节点进行编码，然后用这个编码进行下游其它应用。
在有监督学习中，GNN往往不只是编码，而是把下游任务也一起放进来了（比如一个分类器），从而能用数据集进行有监督的学习。

GNN本质是一个编码：

h_v=f(x_v,x_{co(v)},h_{N(v)}, x_{N(v)})

四个输入分别是：节点自己的特征、节点连接的边的特征、节点的邻居的编码表示、节点的邻居的特征。

GCN#

GCN的形式是这样的：

H^{t+1}=\sigma(\~AH^tW^t) \\ \~A=I_n+D^{-\frac{1}{2}}AD^{-\frac{1}{2}}

这是一个多层的网络，所以有 t+1, t。然后 Wt 是每层的参数。然后矩阵 $\~A$ 其实是一个标准化后的拉普拉斯矩阵，A矩阵是邻接矩阵，D矩阵的图的度矩阵，度矩阵是一个对角矩阵， $D_{ii}$ 为节点 i 的度。 $\sigma$ 是一个激活函数。
这个公式好像没有卷积？需要注意的是，图上的离散卷积和我们平时用在图像上的不太一样，上面这个公式其实是已经进行了卷积、然后不断对这个卷积式子化简后的结果——这个式子直接是卷积的简化后的结果，换句话说，这个式子本身就是图上卷积。

$\~A$ 矩阵是和整个图的结构有关的一个矩阵量。我所理解的 GCN是：给定一个图有n个顶点的图，有了这个图就直接有 $\~A$ 矩阵了，图上每个顶点有自己的初始特征，所有顶点特征向量拼在一起成为第一层的输入矩阵 $H^1$ ，然后进行一次卷积并经过激活函数得到第一层的输出第二层的输入 $H^2=\sigma(\~AH^1W^1)$ （还可以纳入一个bias…），然后继续接下来几层，最后得到输出H，为每个顶点的编码向量。然后用这个编码做下游任务，用下游任务的结果的loss来更新整个网络…

可见，GCN只能用在一个给定的固定的图上。

GCN的核心的图上卷积操作是怎么来的，挺复杂的。

W是否可以用其它网络，而不是一个矩阵相乘呢？

拉普拉斯矩阵#

拉普拉斯矩阵 L 是图论上常用的表示图的一些特点的矩阵，定义为:

L=D-A \\ L_{ij}=\begin{cases} D_{ii}, \quad i=j \\ 1,\quad v_i, v_j 邻接 \\ 0, \quad otherwise \end{cases}

其中D为度矩阵，A为邻接矩阵(不考虑自环，即对角线为0)。

拉普拉斯矩阵有很多性质：

L 是实对称矩阵，可以谱分解 $L=U\Lambda U^T$ ，其中U为正交矩阵，列向量两两正交，每个列向量都是单位向量，逆为自己的转置。 $\Lambda$ 是由 L 的特征值组成的对角阵。
L是半正定的。
特征值中0的个数就是连通分支的个数。
最小特征值为0.
最小非零特征值是图的代数连通度。

拉普拉斯矩阵存在两种标准化形式：

\begin{aligned} L^{sn}&=D^{-\frac{1}{2}}LD^{-\frac{1}{2}} = I-D^{-\frac{1}{2}}AD^{-\frac{1}{2}} \\ L^{sn} &= \begin{cases} 1, &i=j \And D_{ii}\neq 0 \\ -\frac{1}{\sqrt{D_{ii}D_{jj}}}, &i\neq j \And v_i,v_j 不相邻 \\ 0, &otherwise \end{cases} \end{aligned}

这就是我们上面见到的 $\~A$ 。

还有一种 Random Walk Normalization 的，先不管。
每个节点的特征是否可以是高维数据？

图上卷积#

上面那个卷积式子看起来和我们熟悉的卷积八竿子打不着…这其实从原始形式一步步推理简化来的，整个过程还比较复杂。

先空着。

GraphSAGE#

主要看的这个 GraphSAGE简介

GCN只能应对静态图，无法处理动态图（“不能应对归纳问题”），是天然的不利；而且 $\~A$ 矩阵仍旧很大，每次要对整个图进行推理和更新，很难用到大规模数据上。GraphSAGE给出了一种框架，能够应对各种图，并且是局部更新。

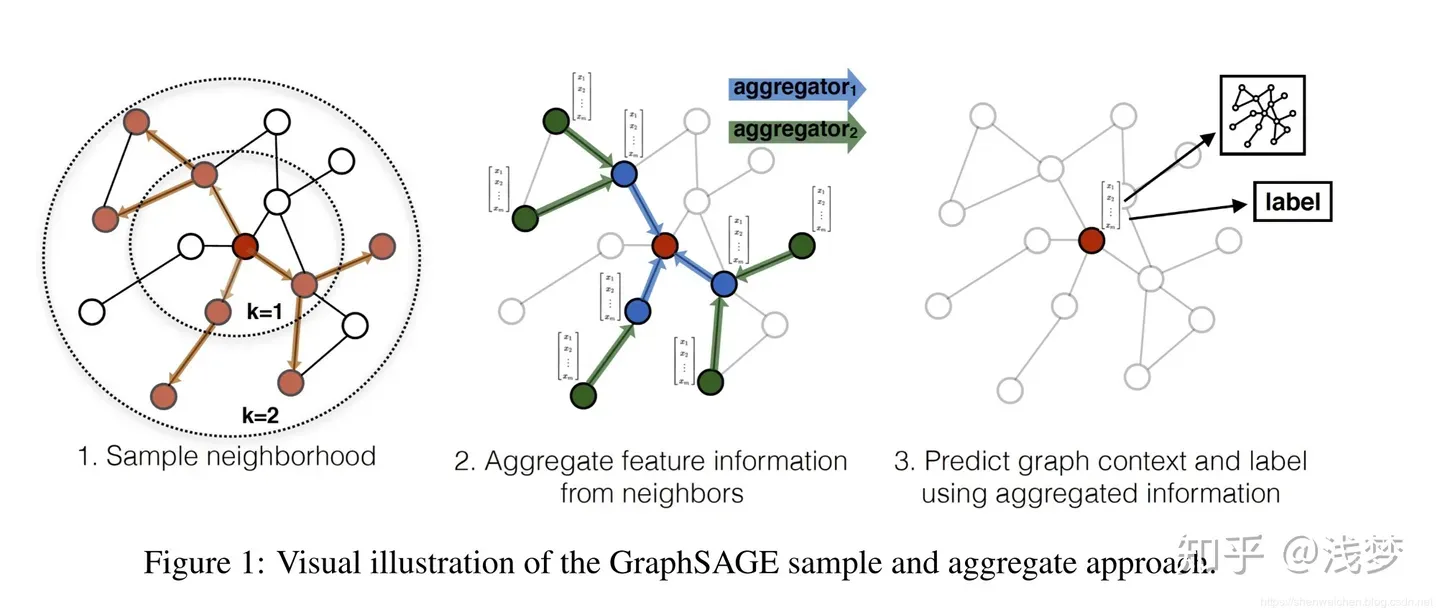
这是一个有一定通用性的框架，它分为三个步骤：

采样。对顶点的邻居采样。
聚合。将采样的邻居的上一轮特征码用一个聚合函数进行聚合，得到邻居聚合码 $h_{N(v)}^k$ 。
更新。将刚刚的聚合结果和自己节点上一轮的编码拼接 $\{h_v^{k-1}||h_{N(v)^k}\}$ ，进行一个变换并经过激活函数后，得到这个节点的新编码 $h_v^k=\sigma(f^k(\{h_v^{k-1}||h_{N(v)^k}\}))$ .

GraphSAGE图示

伪代码如下：

伪代码里更新每个节点的时候用了所有邻居，这就是“无偏”的，在相邻节点比较少、图比较稀疏的时候比较可以用。但当图非常大，一个节点有非常多邻居的时候就比较昂贵了，需要从邻居中采样。此外，最后要对编码进行归一化防止越来越大。

其中 $W^k$ 是一个变换，这里写成了一个参数矩阵相乘，但也可以用GRU，LSTM等，总之是一个函数或者变换。

最外层遍历了K层其实就是说这个网络结构有K层。这个K的值代表最多考虑了与每个节点最短路径为K的邻居。在第K层的时候，可以直接对节点的K跳邻居进行采样、聚合，而在聚合的时候通过一跳邻居进行多次聚合向内传播到正在处理的节点，最后更新节点。上面的图中显示了一个k=2的情况。

比如，一开始，每个节点都只是自己的特征，只考虑了自己。然后做一轮采样聚合更新，每个节点就结合了相邻的那个一跳邻居。进行第二轮采样聚合更新后，每个节点又一次考虑了相邻节点（上一轮）的编码，而这个上一轮编码是考虑了这个相邻节点的相邻节点的，相对于正在被更新的节点就是最多为2跳，所以k为2的时候最多考虑了两跳邻居。

聚合函数Aggregate#

有多种聚合函数，用于聚合步骤，即上面伪代码的第四行。比如MEAN, 比如Pooling，比如 LSTM GRU，甚至图卷积GCN。

Mean Aggregate#

Mean Aggregate直接将聚合更新两个步骤（伪代码的4、5行）混在一起了：

h_v^{k+1}=\sigma(W*Mean(\{h_v^k\}\cup\{h_i^k|i\in N(v)\}))

也就是，直接将自己当前的编码和其邻居的编码求平均，然后经过一个线性变换，最后经过激活函数，就得到新的编码了。

Pooling Aggregate#

这就是上面伪代码单独的第四行了。

h_{N(v)}^{k+1}=max\{\sigma(W_{pool}\times h_{u}^k+b)|u\in N(v)\}

先对每个相邻节点的编码进行一次非线性变换，然后用max pooling或者mean pooling。

图卷积#

以节点为中心对其邻居采样，包括本节点，就形成了一个子图（而且是局部的、比较小的子图），应该就可以图卷积了。

LSTM，GRU#

这类网络，其结果和输入的顺序密切相关。邻居节点的编码一个个先后丢入LSTM后者GRU，而我们知道LSTM和序列输入顺序密切相关，我们不希望聚合函数和邻居顺序有关，所以每次聚合之前要对邻居节点打乱 shuffle。

训练#

有无监督和有监督两种。无监督主要基于下面这个目标函数：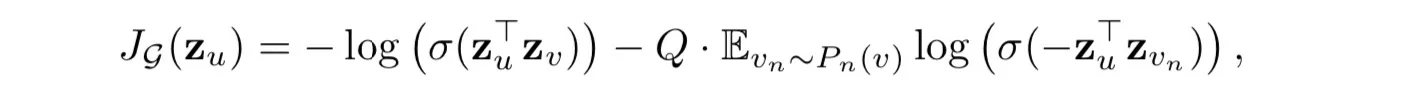
无监督目标函数
其中v是通过固定长度的随机游走出现在u附近的顶点， $p_n$ 是负采样的概率分布， $Q$ 是负样本的数量。——我也不懂。

有监督就是结合下游任务，用有标签的数据集连着GNN和下游网络一起训练，更好理解。

GAT#

GAT, Graph Attention Networks, 主要参考了这个。

顾名思义，就是注意力机制的 GNN——那就比较明确了：注意力就是对输入“序列”的加权和嘛！在GNN、在一个图上，这个“序列”就是一个节点的相邻节点的编码。一个节点的编码要考虑其相邻节点，而哪些邻居对于这个节点比较重要，就应该有更大的权重。注意力就是干这事的。

对于一个节点 i，其相邻节点的权重为：

e_{ij}=a([Wh_i||Wh_j]),\quad j\in N(i)

其中，用一个“共享参数”（所谓共享参数，就是说对于所有的i和j，这一步用的W(注意和下面多头里用的W区分)都是同一个）W 对 hi 和任何相邻节点j的 hj 做变换，然后 concat，最后通过一个 a 函数将向量映射到一个实数eij，对所有邻居做同样的操作，得到每个邻居的权重eij.

回忆，scaled-dot attention 就是QK点乘，然后除以向量维度的开平方，得到一个作为向量的实数。

之后，对于所有 i 的相邻节点的权重，做softmax归一化：

\alpha_{ij}=\frac{\exp(LeakyReLU(e_{ij}))}{\sum_{k\in N(i)}\exp(LeakyReLU(e_{ik}))}

注意这里用了 leakyrelu，一个trick。

最后当然是加权求和：

h_i' = \sigma(\sum_{j\in N(i)}\alpha_{ij}Wh_i)

注意，这里还是需要先用W做一个变换！

当然，注意力还得多头。

h_i' = ||_{k=1}^K\sigma(\sum_{j\in N(i)}\alpha_{ij}^{(k)}W^(k)h_i)

||表示concat！

和自注意力一样，多头始于用K个不同的W对h做变换，进入多个头。

基于类 GraphSAGE 的方法，在两个节点有很多公共邻居的时候，他们的特征表示大多都是由这些公共邻居产生的，那么他们的编码就可能很相似，在层数叠地较多的时候，可能会 over-smooth（有时候这是可以的，但有更多时候这样不好）。