VAE

2024-06-08

概述#

主要学习自VAE introduction from Lil 。本文只是为了梳理、记录我自己的理解以加深印象，大部分内容和图片直接来自于它。

VAE大概是一个典型的自编码结构，先将输入编码到一个潜在空间（特征），然后将这个潜在空间里的潜码解码成原本的结果——这是最基本的自编码器AE；所谓变分自编码器VAE，从它的计算流程简单粗暴地说，就是把源输入编码到一个分布中，这个分布构成了后续解码的潜在空间；解码时，从分布中采样出潜码，直接解码。因此，VAE可以用来生成。

此外，VAE出来的中间结果，也就是那个latent space，从它采样的特征向量的位数一般要远小于原始数据（尤其是图像等），因此可以用来降维、压缩特征、加速其它深度学习结构（比如Diffusion）等。

总之，先把握VAE是一个编解码的结构。先规定一下本文中经常用到的一些数学符号。

符号	意义
$\phi$	编码器网络的参数
$\theta$	解码器网络的参数
$\cal{D}$	数据集 $\cal{D}=\{\bold{x}^{(1)},\dots,\bold{x}^{(2)}\}$ ，有n个samples
$\bold{x}^{(i)}$	每个数据sample是d维向量
$\bold{x}'$	经过一次编解码后重建的 $\bold{x}$
$\bold{z}$	在编解码器中间那个瓶颈中学到的压缩编码，或者潜码，或者其它称呼。
$a_j^{(l)}$	激活函数；在第l个中间层的第j个神经元的激活函数
$g_\phi(\cdot)$	编码器函数（一个网络），参数为 $\phi$
$f_\theta(\cdot)$	解码器函数，参数为 $\theta$
$q_\phi(\bold{z}\\|\bold{x})$	Estimated posterior probability function，用来评估编码器后验概率的函数…这个被当做了后验概率，可能在编码器中，将原数据x当做了果，而编码后的z才是因..? 应用此概率，编码结果是和原数据有关的概率分布，这样的编码器称为概率编码器probabilistic encoder
$p_\theta(\bold{x}\\|\bold{z})$	给出特征码z，解码器有多大的概率得到正确的原数据x？解码器也是个概率分布，这样的模型称为概率解码器probabilistic decoder

自动编码器Autoencoders#

VAE之前是很多各种形式的AE，AE的理论很早，也比较简单，就是典型的输入-神经网络编码器-中间编码（特征码）-神经网络解码器-解码后的输出，让编解码前后的数据尽可能相同。

AutoEncoder#

最朴素直接的自动编码器，就是和上面那一段说的一样。

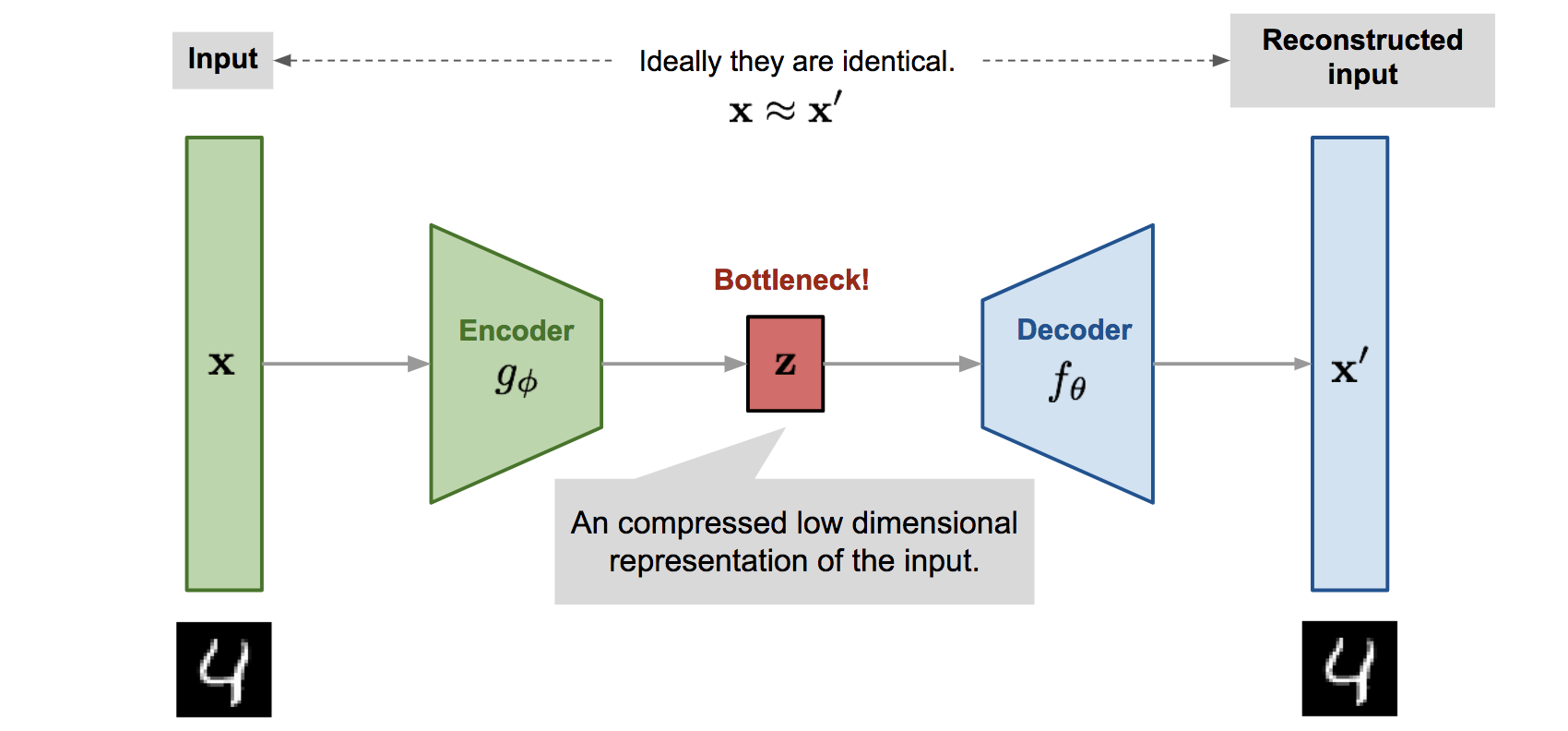
最简单的自编码器

优化目标就是让重建后的 $\bold{x}'$ 和之前的原数据 $\bold{x}$ 一致，就是两者的最小二乘loss：

L_{AE}(\theta,\phi)=\frac{1}{n}\sum_{i=1}^n(\bold{x}^{(i)}-f_\theta(g_\phi(\bold{x}^{(i)})))^2

Denoising AE#

为了解决AE容易过拟合的问题，增强模型的鲁棒性，提出了denoising AE，同样非常早，以后来的眼光看，就是往原数据中加噪声进行数据增强。

Denoising AE随机舍去原数据中的一些像素，变成 $\~\bold{x}\sim\cal{M}_{\cal{D}}(\~\bold{x}|\bold{x})$ ，然后让AE从这个有缺陷的数据恢复原数据。

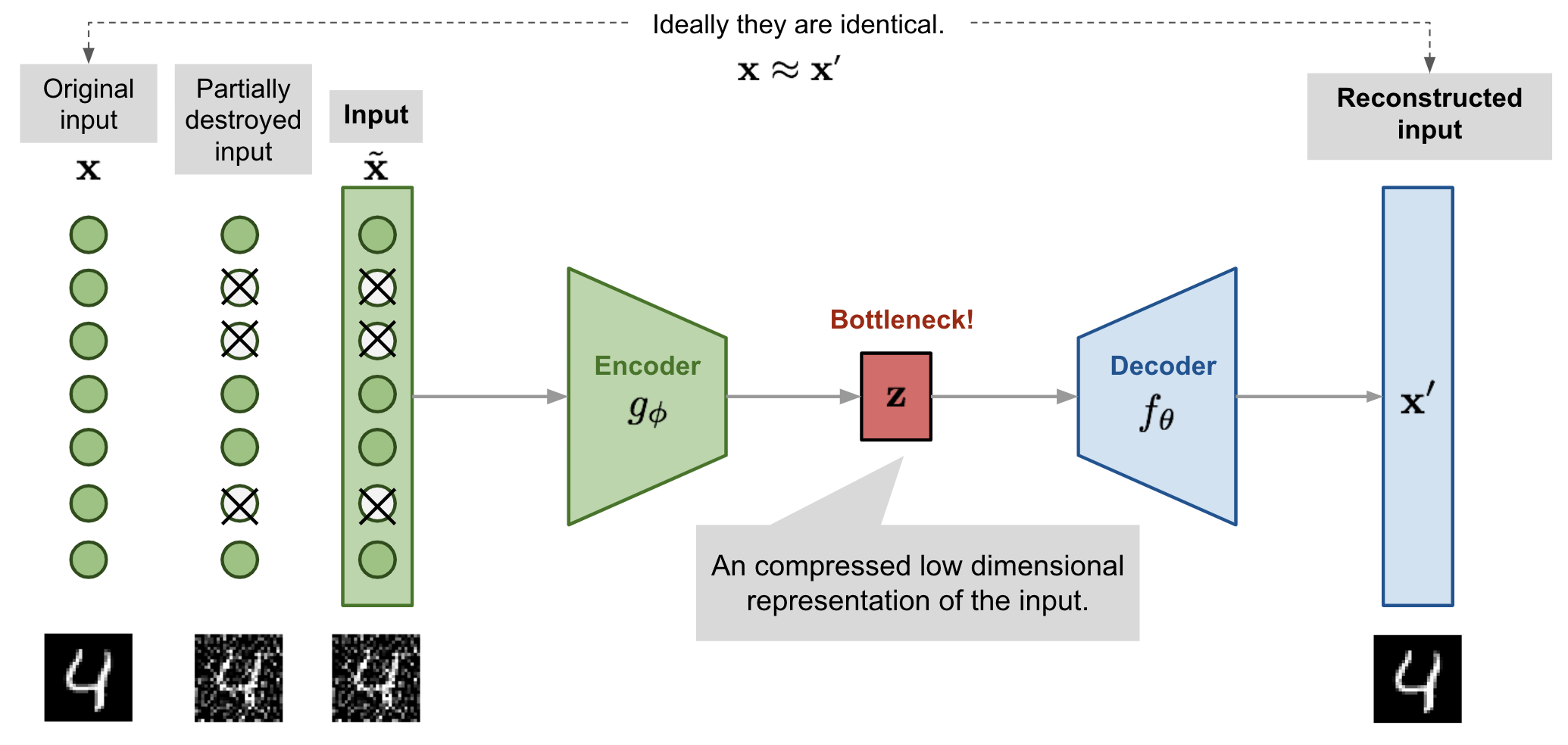
Denoising AE

让人想起ViT骨干模型的训练好像就是把图片的patches挖掉几块（和Bert的完形填空式预训练有点像）。

Sparse AE#

稀疏自编码器同样是为了缓解过拟合和增强鲁棒性，它的思路是对隐藏层中的神经元施加 “稀疏约束”，同一时间只有少量神经元能被激活（神经元输出不为0或较大），神经元在大部分时候都是不激活（神经元输出为0或很小）的。
这是如何约束的？让某个神经元“遍历”数据集中的所有数据，有一些数据能让它激活，另一些不能让它激活，这个约束做的就是只有少量数据能让这个神经元被激活，这个少量可以用比例来控制。大部分激活函数（如sigmoid, tanh等）都是映射到[0, 1]，假设激活的时候是1，不激活的时候是0，计第i个隐藏层中的神经元 j 为 $a_j^{(i)}$ ，稀疏约束可以表示为：

\^\rho_j^{(i)}=\frac{1}{n}\sum_{k=1}^n[a_j^{(i)}(\bold{x^{(k)}})]\approx \rho

$\rho$ 是一个超参数，规定稀疏的程度。但有个问题，某一层神经元的输入是上一层神经元的输出，而不是数据本身，是否要考虑这个？

但这个公式不能直接拿来做loss，将此约束纳入到损失函数中，是通过向损失函数增加一个惩罚项实现的。

\begin{aligned} L_{SAE}(\theta, \phi)&=L(\theta,\phi)+\beta\sum_{l=1}^l\sum_{j=1}^{s_l}D_{KL}(\rho|\^\rho_j^{(l)}) \\ &=L(\theta,\phi)+\beta\sum_{l=1}^l\sum_{j=1}^{s_l}(\rho\log\frac{\rho}{\~\rho_j^{(l)}} + (1-\rho)\log \frac{1-\rho}{1-\^\rho_j^{(l)}}) \end{aligned}

这里把 $\rho$ 当成了分布，然后用了KL散度度量当前的实际 $\rho$ 和阈值之间的差距..

K-Sparse AE#

K-Sparse AE的稀疏作用在中间瓶颈层的特征码 z 上，先正常通过前馈神经网络的编码器得到z，然后只有z中值最大的 K 个元素被保留，其它的直接置0，这可以通过可变阈值的ReLU函数实现。在反向传播的时候，只有没被归0的神经元会继续往编码器中传播梯度。

Contractive AE#

它建议自编码器编码出的结果处于一个“收缩的空间”（contractive space）以保持更强的鲁棒性。且不讨论这里面的数学术语和可能的理论推导，它的做法是往损失函数中加一个惩罚项，降低编码 z 对输入 x 的敏感度。这个惩罚项是编码 z 关于其输入原数据 x 的雅可比矩阵的弗罗贝尼乌斯范数 (Frobenius norm)。雅可比矩阵是结果向量的每个分量对输入向量的每个分量的偏导数，弗罗贝尼乌斯范数就是矩阵中所有项的平方和。

||J_f(\bold{x})||^2_F=\sum_{ij}(\frac{\partial h_j(\bold{x})}{\partial x_i})

其中， $h_j$ 是编码出来的 $\bold{z}$ 的第 j 个分量。

作者称，经验上说，这个损失项带来了一个和低维非线性流形相关的特征表示，而在和流形正交的方向上大致保持不变invariant。

Variational Autoencoder VAE#

VAE框架的由来#

变分自编码器，虽然和自编码器有非常相像的模型结构，但好普通自编码器的理论思路很不一样。它更多来自变分贝叶斯推断理论。

不同于AE，VAE并不试图将输入变换到一个固定的特征向量，而是变换到一个概率分布distribution。VAE的关键是那个“解码器”（参数为 $\theta$ ，把从潜码空间采样的z变换为数据x），所以我们从这个参数为 $\theta$ 的解码器的角度，先做一些定义：

先验Prior， $p_\theta(\bold{z})$ ，采样出 z 的概率；
似然(或是其它翻译？可能性？) Likehood， $p_\theta(\bold{x}|\bold{z})$ ，给出潜码 z 的情况下，生成结果是 x 的概率。
后验 Posterior， $p_\theta(\bold{z}|\bold{x})$ ，生成结果是 x 的情况下，它是由 z 生成出来的概率。

假设我们已经知道最优参数 $\theta^*$ ，我们要用它生成和真实数据 $\bold{x}^{(i)}$ 很相似的数据。首先生成过程是：利用 $\theta^*$ 决定的先验 $p_{\theta^*}(\bold{z})$ 采样出一个编码 $\bold{z}^{(i)}$ ，然后用这个 $\bold{z^{(i)}}$ 生成一个 $\bold{x}$ ，而生成这个 x 的概率是似然函数 $p_{\theta^*}(\bold{x}|\bold{z}=\bold{z}^{(i)})$ 。最后可以表示成 $p_{\theta^*}(\bold{x})=\int p_{\theta^*}(\bold{z})p_{\theta^*}(\bold{x}|\bold{z})d\bold{z}$ 。
最优的 $\theta^*$ 就是让生成结果是数据集中的数据的概率最大：

\begin{aligned} \theta^* &= \argmax_\theta \prod_{i=0}^n p_\theta(\bold{x}^{(i)}) \\ \theta^* &= \argmax_\theta \sum_{i=0}^n\log p_\theta(\bold{x}^{(i)}) \end{aligned}

第二行是取log。然后拆开：

\theta^* = \argmax_\theta \sum_{i=0}^n\log\int p_{\theta^*}(\bold{z})p_{\theta^*}(\bold{x}^{(i)}|\bold{z})d\bold{z}

可以看到，要算 $p_{\theta^*}(\bold{x}^{(i)})$ 很麻烦，不可能遍历所有的 $\bold{z}$ ，所以希望缩窄考虑的z的范围；如果能知道给出 x 的条件下，抽样到某个z的概率，那么我们就能根据这个概率，只关注最重要的，也就是后验概率 $p_{\theta^*}(\bold{z}|\bold{x})$ 。——其实这些说法也只是在根据结果推理由…——我们用一个函数 $q_\phi(\cdot)$ 来拟合这个后验概率，我们发现这个函数做的就是：在给出 $\bold{x}$ 的条件下，预测最可能出现 z，x->z，这不就像是一个“编码器”吗？解码器是从 z 生成 x，而编码器是从 x 猜测 z，这样一个长得和 AE很像的结构就出现了，虽然理论上的意义是完全不同的：VAE中的“编码器” q 实际上是对用于生成的概率函数 (“解码器”) p 的后验概率的拟合。

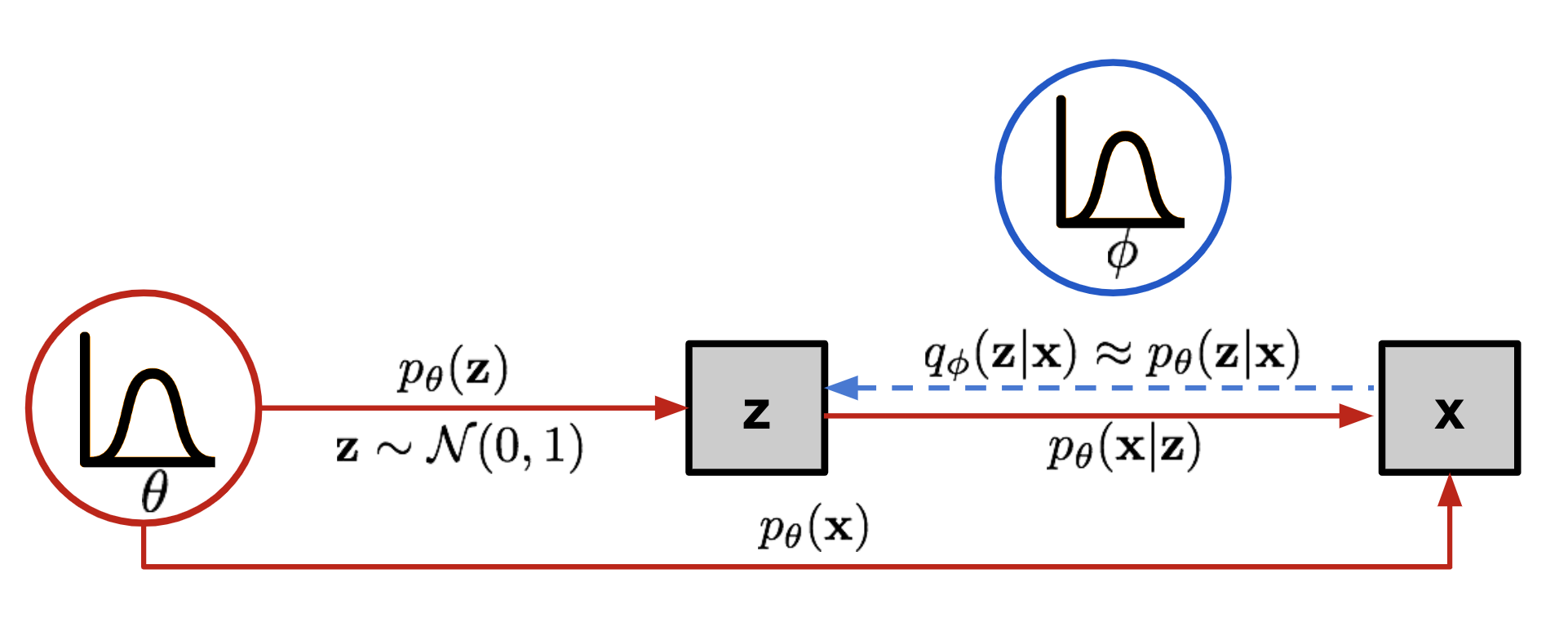
VAE的“编码器”“解码器”

如果把x->z的蓝色虚线展开，放到另一侧，是不是就很想一个 AE 了？

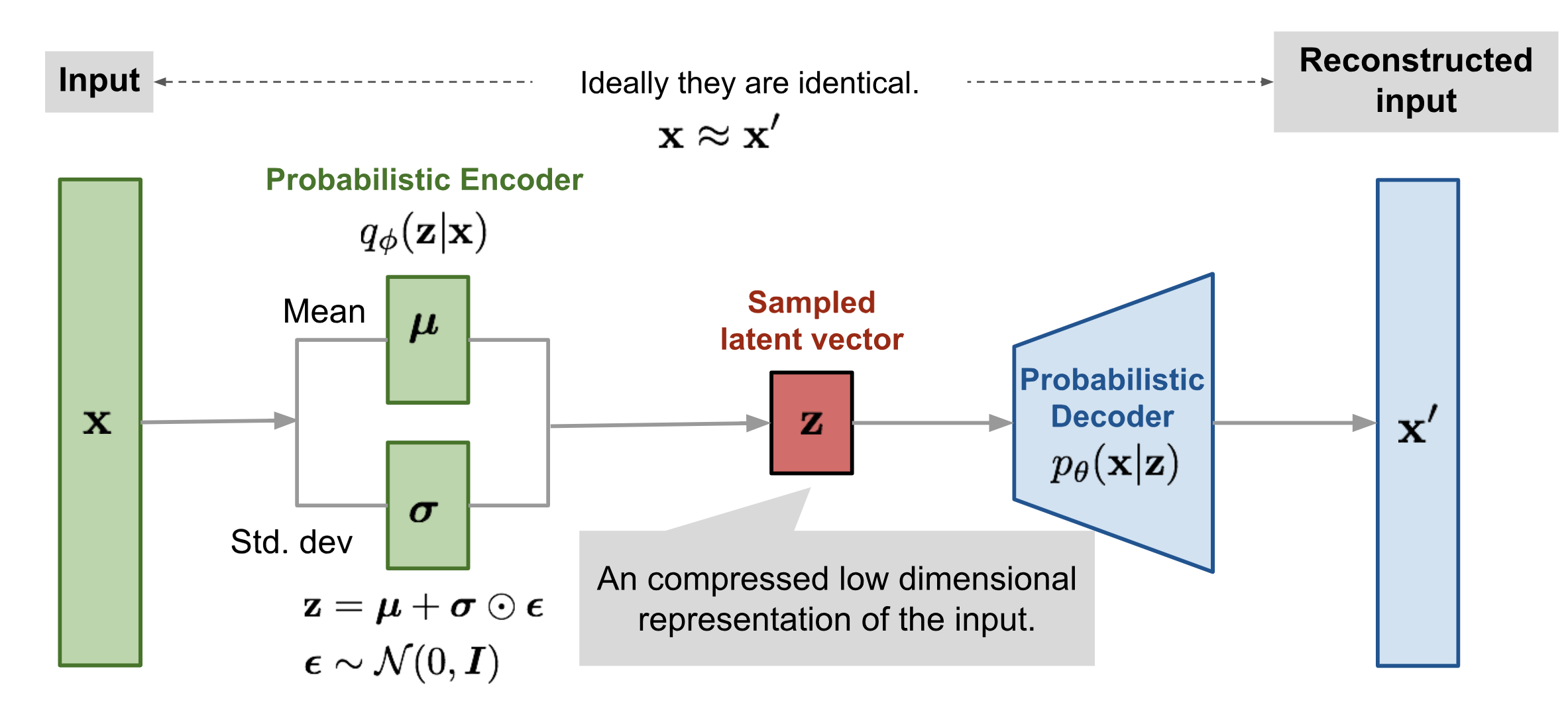
VAE结构图

损失函数 ELBO#

得到了VAE的框架后，下一步就是如何优化它，这里简要地推导VAE的损失函数 ELBO，它非常重要，之后的 Diffusion 也常常见到它的身影。

我们的最终目标是要优化上面那个关于 $\theta^*$ 的式子，也就几优化 $\theta^* = \argmax_\theta \sum_{i=0}^n\log p_\theta(\bold{x}^{(i)})$ ，而ELBO的起点是让后验概率的拟合函数 $q_\phi$ 尽可能接近真正的后验概率（最后推导出和前面的 $p_{\theta^*}(x)$ 有关，很神奇的推导…）
可以用KL散度衡量两个概率分布之间的距离： $D_{KL}(q_\phi,p_\theta)$ ，至于为什么用 KL(Q, P) 而不是用 KL(P, Q)，Lil给了一个网址说他说得很好，但我没看。大致好像是最小化 KL(X, Y) 会导致所有X的概率密度大于0的地方Y的概率密度也大于0（X“覆盖”Y，左边的覆盖右边的），如果一方是“确定”的而另一方是要优化的，把被优化的放在右边，可能导致被优化的只覆盖了一部分，因为即使只覆盖一部分也能满足“左边的覆盖右边的”。
这么说当然是有问题的，但我没有进一步了解。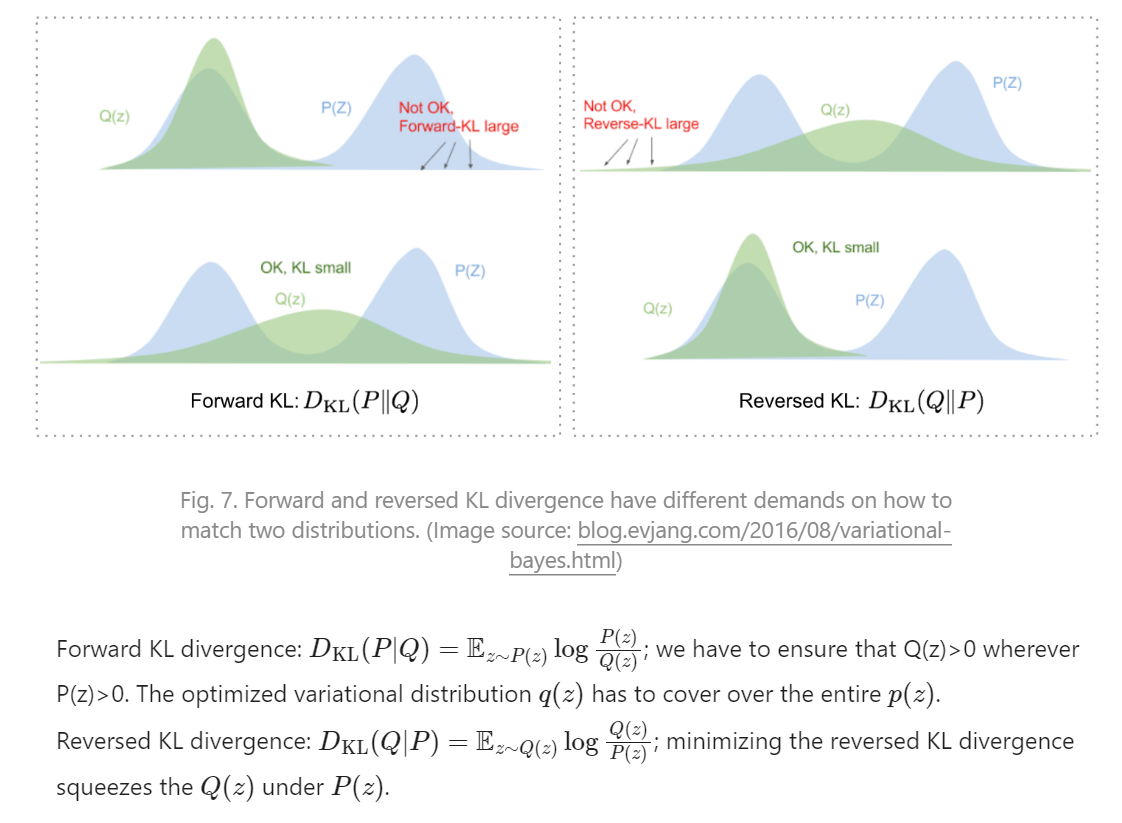
关于KL散度中的Q, P的顺序

总之，我们优化 $D_{KL}(q_\phi, p_\theta)$ ，推导过程如下：
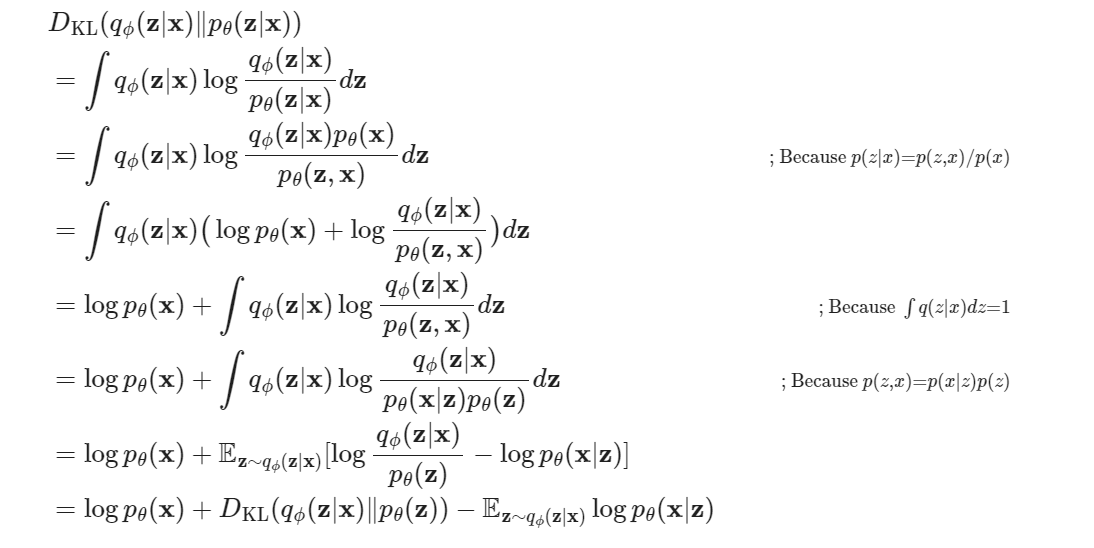
VAE ELBO 推导过程

推导中的第二行，展开KL散度公式。第三行使用条件概率公式，分离我们希望要的那个 p(x)，第四行拆开这个log，把这个p(x)分离出去，第五行分离这个x项离开积分，我们最终需要的 log p(x) 就出来了，之后利用神奇操作又凑出一个KL散度，和一个期望，这个主要是用到那个期望，因为期望中的q, p都是我们知道的（也就是网络本身），它是可以直接用来后续优化的（原先KL散度中的p后验是用不了的，因为不知道）…

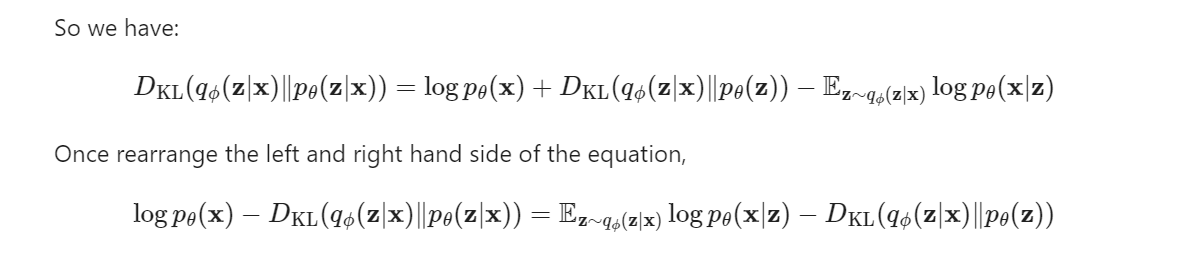
最后的推导结果

发现这里面就包含了我们最终需要的 log p(x)，然后移项，定义最终的Loss如下：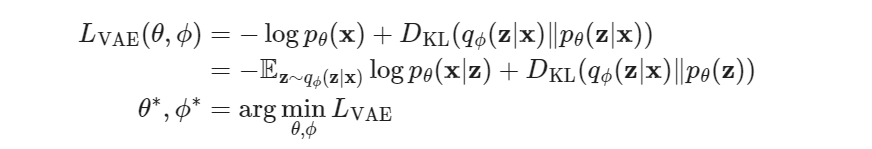
Loss VAE

第一行是原始形式，主要是 log p(x)（将它最大化），右边那个是为了能够计算（用上面的推导），第二行代入了上面的推导结果，得到了期望和KL散度。
那个期望似乎是： $E=\int q(z|x)\log p(x|z)dz$ ，这东西的直观意义是：最大化在q(z|x)这个分布下log p(x|z)的期望，也就是如果我已经把x输入q得到了z，那么我在p(x|z)下的概率也应该大——把z输入p能得到和原本接近的x，可以基于此简化损失函数。
实际使用的时候会优化第二行的第二项吗？ 这个先验 p(z) 可知吗？还是说，只优化第二行的第一项？——会。实用中一般会假设z服从标准正态分布，因而可算。

上面的损失函数叫 变分下界variational lower bound，因为（注意KL散度是非负的）：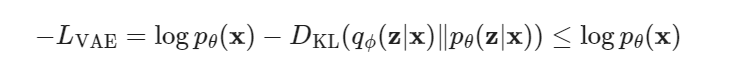

最小化 LVAE 实际上是在加大最终优化目标 log p(x) 的下界，所以成为变分下界。

实用中VAE的损失函数#

2我们最终要优化 p(x)，而在上一小节中， $L_{VAE}$ 最后化成了两项： $E_{z\sim q_\phi (z|x)}\log p_\theta(x|z)$ 和一个KL散度衡量p的先验（p(z)）和用于估计后验p(z|x)的网络 $q_\phi(z|x)$ 之间的差异。一项一项说。

对于第一项，那个期望，最小化 $L_{VAE}$ 就是最大化这个期望，最大化这个期望的意义，用自然语言大概解释就是（当然，这不准确），如果Q网络从x得到了z，那么P网络要尽量能从z得到x（所谓尽量就是概率尽可能大）——这不就是 $x'\approx x$ ？所以在实用中，第一项直接变成了原数据x和经过VAE生成后的x’之间的MSE误差： $MSE(\bold{x}, p_\theta (q_\phi(\bold{x})))$ 。

第二项那个KL散度，我们一般直接假设 z 的分布是一个标准正态分布（所以知道为什么要把 p(z) 叫“先验”…），而 $q_\phi(z|x)$ 也是一个正态分布，也就是这个 q 网络实际上推理了正态分布的期望 $\mu$ 和标准差 $\sigma$ ，q 网络就是用来拟合后验 p(z|x) 的，把那个x给定后，q就可以当做是一个分布了，因为 $\mu, \sigma$ 已经推理出来了，这个确定的q的分布要尽量和 z 的先验接近：标准正态分布，那么第二项就变成了： $D_{KL}(\cal{N}(\mu_\phi,\sigma_\phi^2 || \cal{N}(0, 1))$ 。
值得一提的是，网上有很多博客没有经过上面的变分下界的推导，而把这第二项这个KL散度解释为：由于第一项MSE会导致x和x’越来越像，模型趋于变成确定的（ $\sigma$ 接近0），违背了VAE的初衷，所以我们要加个和标准正态分布的 KL 散度，让q确实推理出一个正态分布（而不是确定值）。——这么说当然有道理，但理论上应该是以变分下界推导为先，这个防止模型变成确定性模型，只是一个恰到好处的副作用。

实际使用的损失函数为：

L_{VAE}=MSE(\bold{x}, p_\theta (q_\phi(\bold{x})))+D_{KL}(\cal{N}(\mu_\phi,\sigma_\phi^2 || \cal{N}(0, 1))

正态分布和标准正态分布的KL散度可以化简，网上有不少博客有推导，自行查找（一般找VAE的损失函数就可以找到）：

D_{KL}(\cal{N}(\mu,\sigma)||\cal{N}(0,1))=-\frac{1}{2}(\log\sigma^2-\sigma^2-\mu^2+1)

所以实用中常用的VAE Loss：

L_{VAE}=MSE(\bold{x}, p_\theta (q_\phi(\bold{x})))-\frac{1}{2}(\log\sigma^2-\sigma^2-\mu^2+1)

重参数(Reparameterize)技巧#

从上面的VAE结构图可以看出，中间有一步是要对分布做采样，但采样这一步是无法求梯度的，也就断掉了反向传播链条。重参数技巧解决这个问题。
由于一般分布用的都是正态分布，正态分布一个很好的性质就是任何mu, sigma的正态分布都可以从标准正态分布N(0, 1)变过去，所以我们的Q只用推出 mu, sigma，然后在标准正态分布上采样，将采样结果乘以标准差加上期望即可，这样采样一步和神经网络没关系了，采样的结果相当于一个常数，不影响求梯度，所以反向传播可以正常进行了。

C-VAE#

AE可以对数据进行降维压缩，但不能生成没见过的数据。VAE可以从一个分布中生成没见过的数据，但是不能控制生成的内容。条件VAE C-VAE试图对生成的内容加以控制。

加入控制的方法很简单，就是在Q, P的输入上分别加入控制参数即可。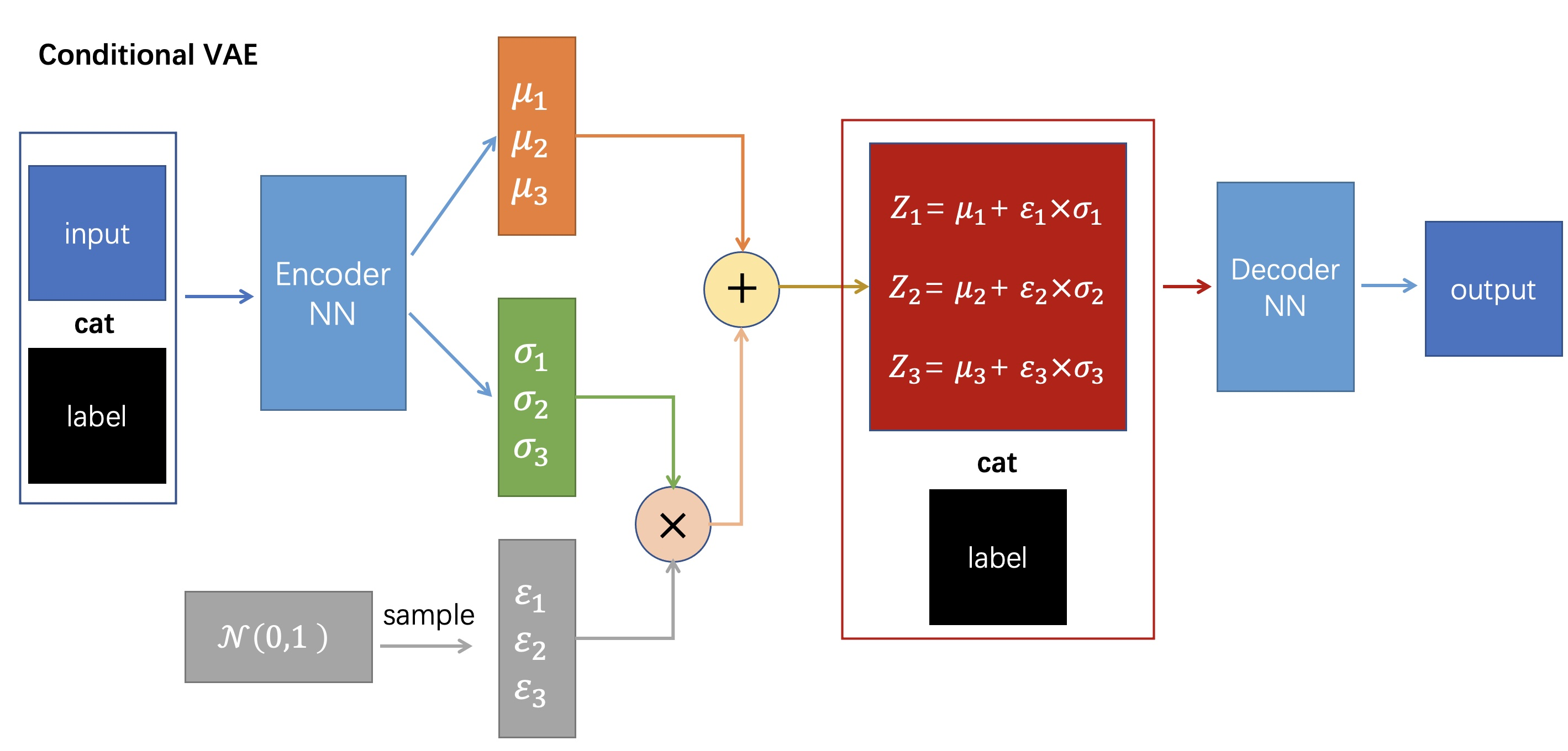
CVAE结构图
比如上面这个结构图，控制参数是它的标签label，在Q网络输入时带上控制参数label，在P网络输入z时也带上控制参数label，即可。控制参数可以是label，可以是其它东西，比如文本生成的CLIP等等…