GAN

2024-06-08

主要学习自GAN introduction from Lil。本文只是为了梳理、记录我自己的理解以加深印象，大部分内容和图片直接来自于它。
本文加入了一些自己的不成熟的理解，建议去看原博客，或看原论文以免被误导。
这篇post本身也已经很早了，17-18年的，内容远非最新进展。当然由于主要讨论数学原理，所以不会过时。

概述#

生成对抗网络受启发与博弈理论，为了生成足够以假乱真的生成结果，使用一个生成器和辨别器进行博弈，生成器生成越发逼真的数据以欺骗辨别器，辨别器学习生成数据和真实数据的差异以辨别真假数据，两者在左右互搏中不断进步，最后丢掉辨别器，得到那个能以假乱真的强大生成器。

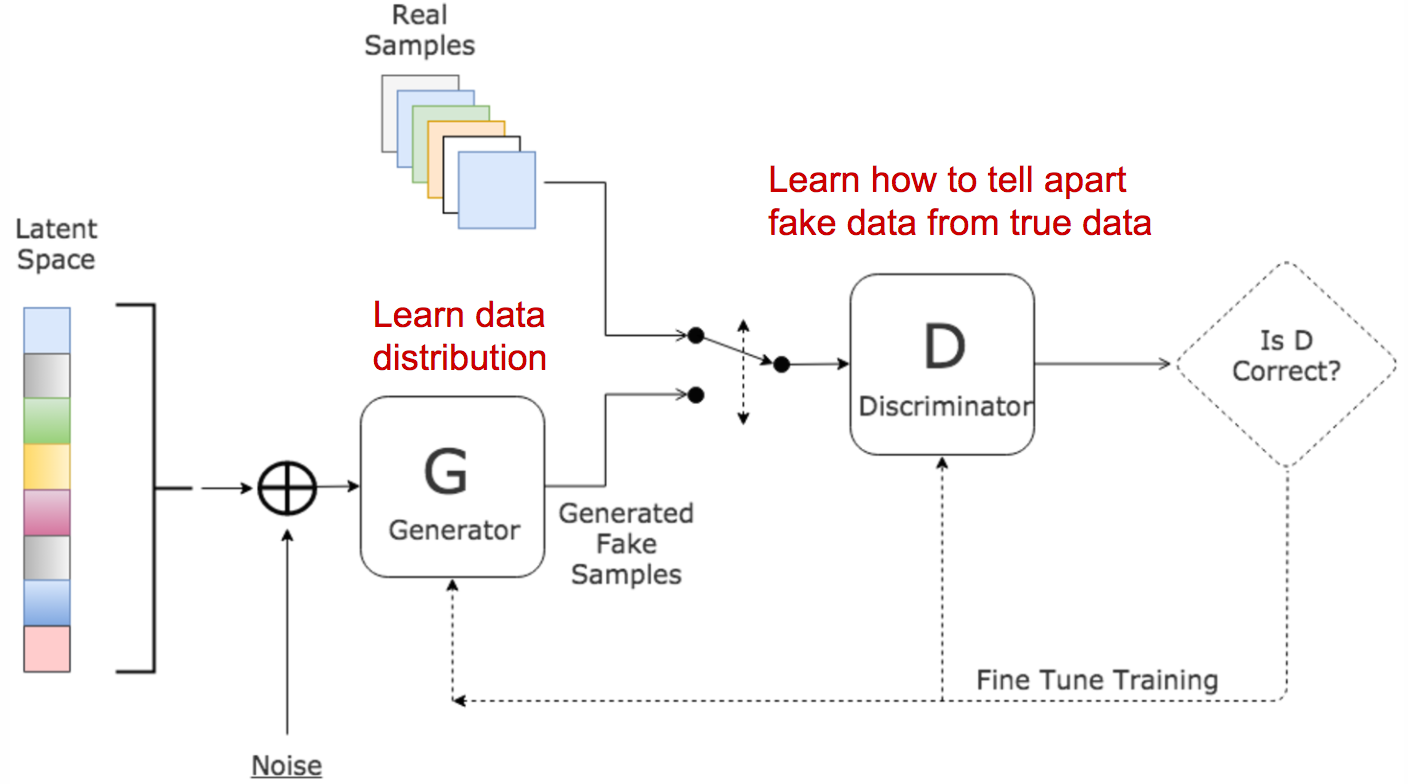
GAN结构

本文关注GAN背后的数学原理，而不是具体的各种五花八门的GAN网络。

数学前置#

KL散度 Kullback–Leibler Divergence#

KL散度 $D_{KL}(P||Q)$ 用来衡量两个分布的距离，即 P （概率密度）和 Q （概率密度）有多大差距、分歧。公式：

D_{KL}(p||q)=\int_x p(x)\log\frac{p(x)}{q(x)}dx

当p, q完全相同的时候，KL散度最小，为0.

KL散度的P和Q 重要性是有区别的，从公式可以看出，如果p(x)接近0，那么q(x)必然大于0，右边（q）的值是被左边（p）制约的，左边的重要性或者“自由程度”大于右边，所以算两个分布之间的差异时，KL散度中的左右顺序不是那么随意的，一般更重要的那个（要优化的那个）放左边。如果两个都一样重要，都要优化，那可能会有问题。

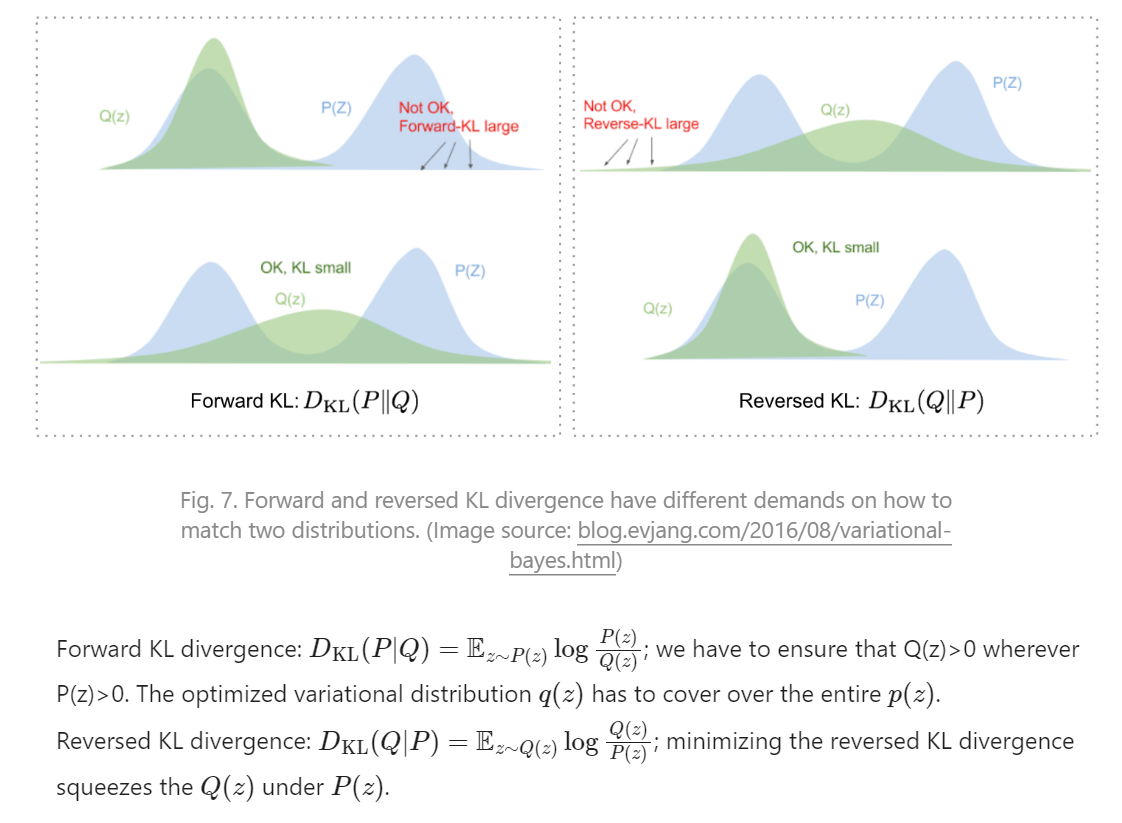
关于KL散度中的Q, P的顺序，假设我们需要优化 Q，让它和P尽量接近
（上图假设要优化Q）

Jensen–Shannon Divergence#

JS散度是另一个衡量两个分布之间距离的方法，它基于KL散度：

D_{JS}(p||q)=\frac{1}{2}D_{KL}(p||\frac{p+q}{2})+\frac{1}{2}D_{KL}(q||\frac{p+q}{2})

JS散度的范围是[0,1]，它有个很大的优势是JS散度中PQ的地位是相同的、对称的。有人认为GAN的成功在于用JS散度替代了KL散度，来衡量两个分布间的距离。

GAN#

GAN的优化目标#

GAN的优化目标很明确、简单，也好理解。
GAN的典型结构如最上面那个图所示。生成器 $G$ 努力欺骗辨别器 $D$ ，而辨别器 $D$ 努力不被欺骗，这是一个零和博弈。
给定符号：

符号	意义	标注
$p_z$	输入的噪声z的分布	一般就是均匀分布
$p_g$	生成器生成的数据的分布，生成数据是x的概率密度。G依赖 $p_z$ 的采样的作为输入，所以这个分布受 $p_z$ 影响
$p_r$	真实数据的分布，真实数据是x的概率密度

D(x)需要把真实的x认为是真（1），而虚假的x认为是假（0）。所以一方面，D要尽量把真的认成真：

\begin{aligned} &\prod_{x\in dataset} D(x) \\ &\sum_{x\in dataset}\log D(x) \\ &\int_x p_r(x)\log D(x)dx \\ &E_{x\sim p_r(x)}\log D(x) \end{aligned}

也就是最大化 $E_{x\sim p_r(x)}\log D(x)$ 。
另一方面，类似的，把虚假的数据 G(z)（z是从 $p_z$ 中采样来的G的输入）辨别为假的：最大化 $E_{z\sim p_z(z)}[\log(1-D(G(z)))]$

而生成器G的目标就是相反，要最小化上面两项。

故而，最终G, D形成了一个最大化最小化（minimax）博弈：

\begin{aligned} \min_G\max_D L(D,G)&=E_{x\sim p_r(x)}\log D(x) + E_{z\sim p_z(z)}\log(1-D(G(z))) \\ &=E_{x\sim p_r(x)}\log D(x) + E_{z\sim p_g(x)}\log(1-D(x)) \end{aligned}

以上更多是针对D而言的。我们最终需要的是G，让G尽可能以假乱真，就是让 $p_g(x)$ 尽量和 $p_r(x)$ 一致。

解析GAN的损失函数#

上面的 $L(G,D)$ 就是损失函数的理论形式。它可以解释地非常直白通俗，但这里将从理论角度上更深入地解析这个损失函数：优化这个 $L(G,D)$ ，实际上优化了什么。

拆解问题，只考虑D，给定x，最优的D(x)是什么？#

L(G,D)=\int_x(p_r(x)\log D(x)+p_g(x)\log (1-D(x)))dx

假设： $\~x=D(x),A=p_r(x),B=p_g(x)$ ，有：
由于x需要遍历，所以我们可以先考虑一个固定的x，只考虑积分内的东西而不考虑积分，如何取D(x)（ $\~x$ ）的值让积分内的这个式子最大？

\begin{aligned} f(\~x)&=A\log\~x+B\log(1-\~x) \\ \frac{df(\~x)}{d\~x}&=A\frac{1}{\~x\ln 10}-B\frac{1}{(1-\~x)\ln 10} \\ \frac{df(\~x)}{d\~x}&=\frac{1}{\ln10}\frac{A-(A+B)\~x}{\~x(1-\~x)} \end{aligned}

令 $\frac{df(\~x)}{d\~x}=0$ ，有：

D^*(x)=\~x^*=\frac{A}{A+B}=\frac{p_r(x)}{p_r(x)+p_g(x)}

最优化了积分内的东西，考虑上积分#

对于任意x，我们知道了D(x)的取值需要为多少来最大化积分内的东西。进一步考虑生成器G，在最理想（也就是对于G来说的最优）情况下，G完全能以假乱真，那么 $p_g(x)=p_r(x)$ ，此时 $D^*(x)=\frac{1}{2}$ ，则式子变成了：

\begin{aligned} L(G,D)&=\int_x (p_r(x)\log\frac{1}{2}+p_g(x)\log\frac{1}{2})dx \\ L(G,D)&=-2\log2\int_x p_r(x)dx = -2\log2 \end{aligned}

变成一个常数了。

不论 G 是否达到最优（也就是 $p_g=p_r$ ），给定生成器G和真实数据R后，D(x) 的值对于每个x来说都是确定的——D(x)的取值看起来是封闭形式！——虽然 $p_g(x),p_r(x)$ 算不了。

进一步：以G的目标的角度#

不要忘记：GAN最终需要的是生成器G，它的优化目标是让生成的结果以假乱真，也就是让 $p_g$ 尽可能和真实分布 $p_r$ 一致，使用 JS 散度而非 KL 散度计算这两个分布之间的距离：

\begin{aligned} D_{JS}(p_r||p_g)=&(\frac{1}{2}D_{KL}(p_r||\frac{p_r+p_g}{2})+\frac{1}{2}D_{KL}(p_g||\frac{p_r+p_g}{2})) \\ =&\frac{1}{2}(\log2+\int_x p_r(x)\log\frac{p_r(x)}{p_r(x)+p_g(x)}dx) + \\ &\frac{1}{2}(\log2+\int_x p_g(x)\log\frac{p_g(x)}{p_r(x)+p_g(x)}dx) \\ =&\frac{1}{2}(2\log2+\int_x(p_r(x)\log D^*(x)+p_g(x)\log(1-D^*(x)))dx) \\ =&\log2 + \frac{1}{2}L(G,D^*) \end{aligned}

上面的推导中，第一步是直接把KL散度写出来，然后将log中的常数2分离出来。然后代入给定G时最优的 $D^*(x)=\frac{p_r(x)}{p_r(x)+p_g(x)}$ .

于是，前面的 $L(C,D^*)$ 可以用JS散度表示为：

L(G, D^*)=2D_{JS}(p_r||p_g)-2\log2

所以，优化 $L(G,D)$ 就是在优化 $D_{JS}(p_r||p_g)$ ，也就是让 $p_g$ 越来越接近 $p_r$ ，越来越以假乱真。

实际使用的GAN损失函数#

前面的更多是对GAN的优化目标的 $L(G,D)$ 的分析，这里简单介绍下实现中GAN的损失函数形式（仅最基本的一种）。

首先，优化生成器就是让 $D(\~x)=D(G(z))$ 尽量接近 1。

\begin{aligned} L_G=&E_{z\sim p_z(z)}[-\log D(G(z))] \\ =&\int_z p(z)(-\log D(G(z)))dz \\ \Rightarrow & \frac{1}{n}\sum_{i=1}^n -\log D(G(z)) \\ =&-\frac{1}{n}\sum_{i=1}^n [\log D(G(z_i))+(1-1)\log (1-D(G(z_i)))] \\ =&BCE(D(G(z_i)), 1) \end{aligned}

第三行那个 $\Rightarrow$ 可能是 $z$ 一般取简单的均匀分布，直接离散化了。BCE是二元交叉熵 $BCE(\bold{x},\bold{y})=-\frac{1}{n}\sum_{i=1}^n (y\log x+(1-y)\log(1-x))$ .

优化辨别器（此时G时确定的，所以有一组生成的结果 $\^\bold{x}$ ）就直接是基于那个 $L(G,D)$ 之D：

\begin{aligned} L_D=&-(E_{x\sim p_r(x)}[\log D(x)]+E_{\^x\sim p_g(\^x)}[\log(1-D(\^x)])) \\ \Rightarrow & -\frac{1}{n}\sum_{i=1}^n (\log D(x_i)+\log(1-D(\^x_i))) \\ =& BCE(D(x), 1)+BCE(D(\^x),0) \end{aligned}

$x\sim p_r(x)$ 是在离散的数据集中均匀随机采样，生成的那组 $\^x$ 也做均匀采样假设…?

GAN 的诸多难题#

不稳定，难收敛#

难训练是GAN的老大难问题。它是两个网络对抗式学习，想要收敛就需要达到一定程度的纳什均衡。而这非常困难。对GAN的训练情况做一点简化，假设两个方程 $f_1,f_2$ ，模型x负责最小化 $f_1(x)=xy$ ，模型y需要最小化 $f_2(y)=-xy$ （形成对抗）。
使用梯度下降去优化， $\frac{\partial f_1}{\partial x}=y,\frac{\partial f_2}{\partial y}=-x$ ，学习率都为 $\eta$ ，那么更新 $x=x-\eta y,y=y+\eta x$ ，最后的结果大概会是这样震荡的情况，难以收敛：
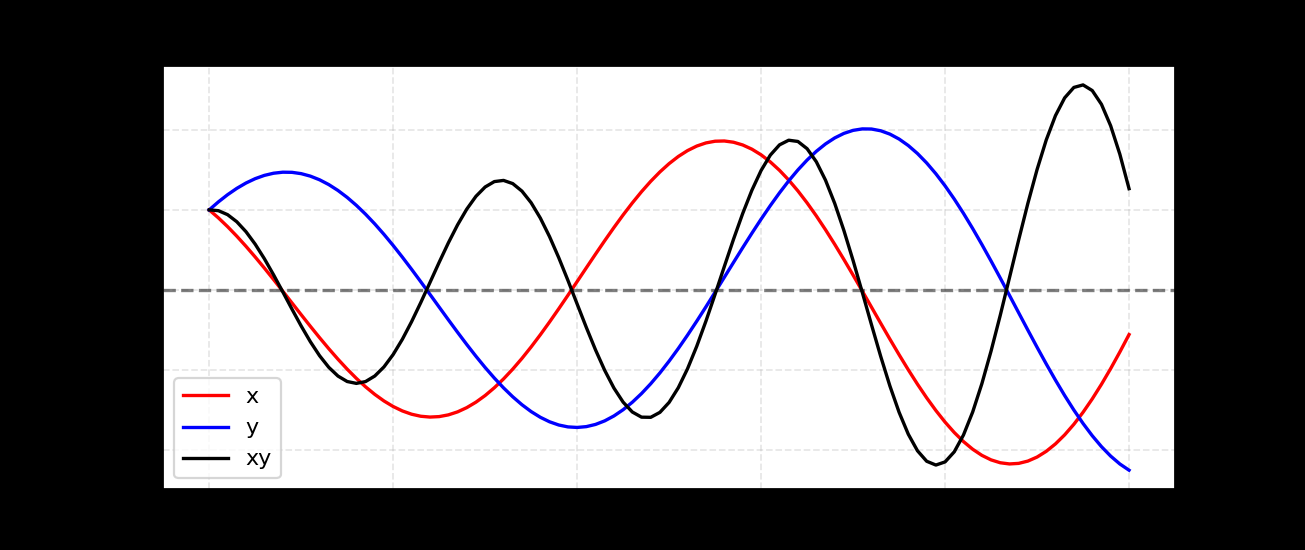
GAN难以达到纳什均衡

低维Supports#

未弄懂，这节可以跳过。

这个东西很理论，我也没仔细了解。这里用到了流形（Manifold）和支持（Support）的概念，我还不太懂。理论来自TOWARDS PRINCIPLED METHODS FOR TRAINING GAN，非常理论。

术语	我也不懂的解释
Manifold	一个拓扑空间，在每个点附近都有接近欧拉空间的性质。如果是n维的就称为n维流形
Support	有一个实值函数f，它把定义域内的数映射到值域中，Support包含了定义域中所有没被映射到0的数

这个解释大概是不对的，我也不知道和后面的结论有什么关系，数学还是薄弱。（至少先看看wiki罢… manifold，support）。

认为 $p_r,p_g$ 都是建立在一个低维的流形上的，这会导致instability。
实际数据集 $p_r$ 的维度可能被高估了，比如说，一张图片看似有几千万像素、几千万的维度，但实际上重要的只是个低维流形——“自由度”没有想象中的那么高——这实际上是流形学习的一个基本假设。
想象一些现实的图片，如果给定一个主题，比如猫、狗，那么画面内容就在很大程度上被限制了，有一个或多个对象主体，有两只眼睛一张嘴，猫猫狗狗的长相也相对接近一个style，这些限制导致图片并非有我们想象中的高自由度——并非每个像素都是自由的。

$p_g$ 也是基于一个低维流形的，这个就好理解，取决于那个随机采样的 $z$ ，它的维度并不高，要知道一个64*64 的图片就有4096个点了！如果用100维的 $z$ 取生成低至 64*64 的图片，这4096个点就要由一个100维的 $z$ 去生成， $z$ 带来的可能性也许无法填满像素空间。

文章指出，既然 $p_r,p_g$ 都基于低维的流形，低维的流形在高维空间中非常可能会脱节、完全不相交（想象两条直线在三维空间中，它远比三维空间中的两个平面更容易不相交），不相交时，理论上可以证明必定能找到一个辨别器 D，100%正确地区分真假数据。而一旦这个D 100% 正确了，就无法训练 G（梯度消失），那么这个网络就无法继续训练了。

梯度消失#

GAN的梯度消失问题更加严重。一个完美的辨别器 D，完全正确地辨别真假数据，那么损失函数 $L(G,D)$ 的值就会是0，无法产生任何梯度。辨别器D越强，L越接近0，G就越会梯度消失。这使得GAN陷入了两难困境：要训练靠谱的G，D就必须也靠谱、也厉害；D一旦优化地强大了，G梯度消失无法训练了。

模式崩溃Mode collapse#

实际使用中，往往发现GAN容易倾向只生成很少数几类的图片，虽然它非常真实，也能骗过辨别器，但它只能生成这少数的几类，无法使用。生成器G容易陷入很狭窄的分布，难以学习复杂的真实世界多变化的数据。

什么时候停止训练？#

GAN没有什么客观的指标，G，D都只在各自的视角下往着欺骗对方的目的走，但G生成的结果是给人看的，什么时候训练好了？不知道。

提升GAN训练的Tricks#

Lil’log 总结自 Improved Techniques for training GAN, TOWARDS PRINCIPLED METHODS FOR TRAINING GAN。

Feature Matching#

不直接分辨真假数据本身，而是分辨真假数据的特征，优化目标为：

\min |E_{x\sim p_r(x)}f(x)-E_{z\sim p_z(z)}f(G(z))|

其中 f 用来算数据的特征，可以自行定义。这样D分辨的也不是数据本身，而是f(x), f(G(x)) 数据的特征。

Minibatch Discrimination#

以前一个minibatch里的数据是互相独立的，minibatch discrimination试图让GAN学习batch里数据之间的关系，我们估算batch里任意两对数据之间的相似度 $c(x_i,x_j)$ ，然后把一个数据与其他所有数据的相似度加起来 $o(x_i)=\sum_j c(x_i,x_j)$ ，这成为数据 $x_i$ 的新特征，一起输入到辨别器中。

Historical Averaging#

对G,D，都往损失函数里加一个惩罚项： $|\Theta-\frac{1}{t}\sum_{i=1}^t\Theta_i|$ ，其中 $\Theta$ 是模型参数，而 $\Theta_i$ 是前i次迭代的时候的模型参数。这个惩罚项可以防止模型一次更新太多，变化太剧烈。
(RNN中常用的clip_norm_，Gradient Penalty?)

One-sided Label Smoothing#

经验上，相比给辨别器0-1标签，给 0.9, 0.1 这样连续的平滑标签似乎能降低模型的敏感性。

Virtual Batch Normalization (VBN)#

在做batchnorm的时候，不根据自己minibatch的数据去做，而是用一个 fixed batch，或者说 reference batch 的数据去做。也就是说，全场用固定的均值和标准差做batchnorm，这个固定的均值和方差来自那个 reference batch，reference batch只在训练开始的时候选择一次。

加噪声#

因为 $p_r,p_g$ 基于低维流形，使得容易优化出特别好的D，造成G的梯度消失，所以可以认为提升流形维度。一个做法是往 D 的输入中加噪声。

使用更好的分布相似性度量#

普通的GAN（前面一直说的那个 $L(G,D)$ ）实际上是在减小 $p_r,p_g$ 之间的JS散度，但是“当两个分部彻底不相交”的时候，这个度量没有意义。

于是有了用 Wasserstein metric（Wasserstein distance）替代 JS 散度。

Wasserstein GAN#

Wasserstein距离又称为Earth Mover’s distance， EM距离，它的定义是要把分布 P和分布Q 的形状通过移动概率密度函数中的值变为一样，最小要移动多少。也就是说，要对P和Q的概率密度函数加加减减多少数，并且乘以这些数在横坐标之间的移动距离，才能把他俩的概率密度函数变为一样。（让我想到了编辑距离：)）。

为了便于理解，先用个离散的例子：P, Q 两列物品，每列4个堆，每堆里有不同数量的物品（每列的物品总数一样），可以在同列的堆之间转移物品，要把P列和Q列的物品分布变得完全一样，假设 $f(i,j)$ 表示从位置i移动了多少物体到位置j，求任意方案下所能达到的最小的 $\sum |f(i,j)(i-j)|$ 。注意考虑移动距离！

列	堆1	堆2	堆3	堆4
P	3	2	1	4
Q	1	2	4	3

一种方案是每次让第 i 堆相同，往第 i+1 堆移动物品：
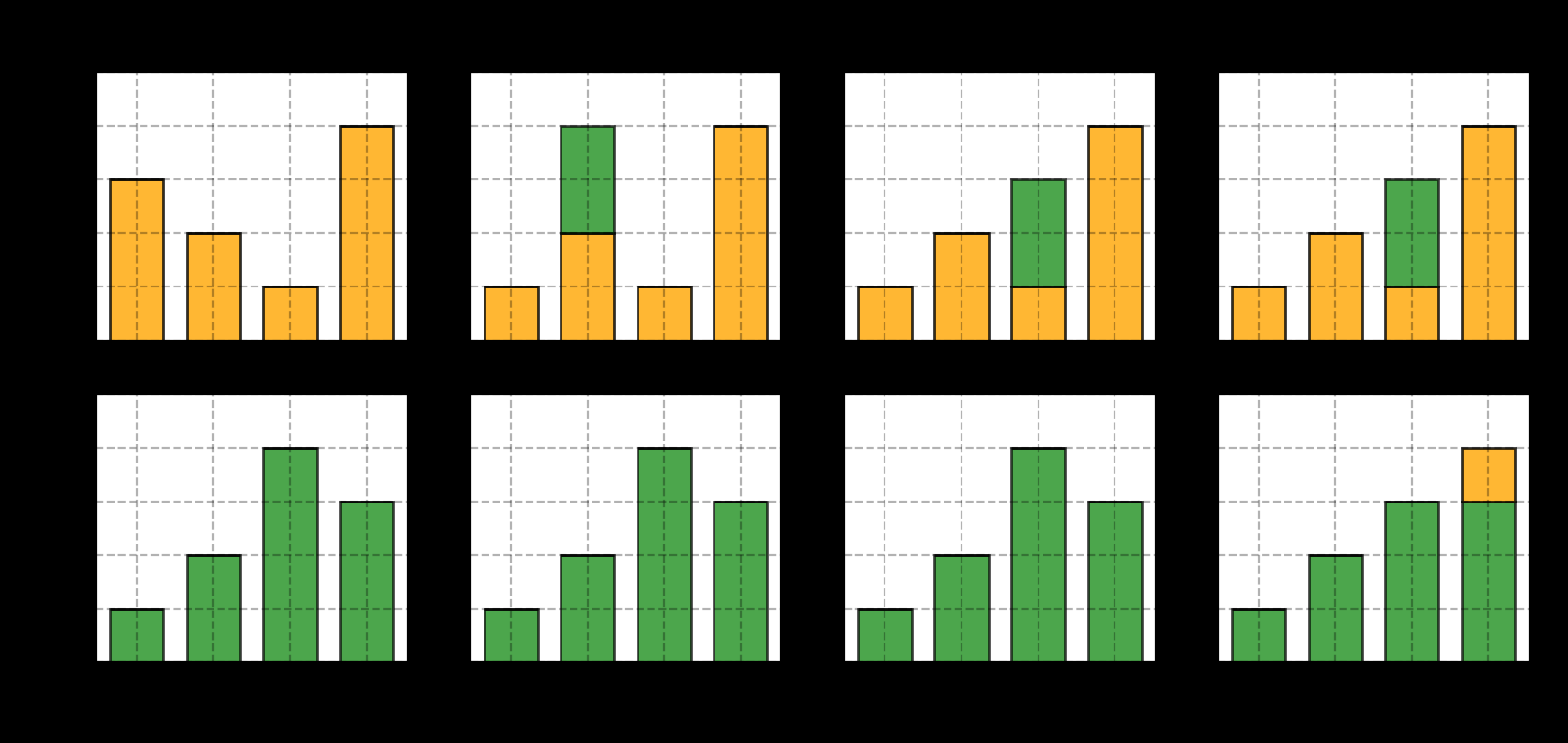
EM距离方案之一
每步移动 0, 2, 2, 1 个方块，EM距离就是 5. 当然，这个简单的例子中没有考虑求最优。

连续情况下，Wasserstein距离定义为：

W(p_r,p_g)=\inf_{\gamma\sim \prod(p_r,p_g)} E_{(x,y)\sim\gamma}|x-y|

其中 $\inf$ 表示最大下界（infimum，回去复习数分Orz）（即所有可能的方案中最小的那种）， $\prod(p_r,p_g)$ 是 $p_r,p_g$ 两者所可能组成的所有联合分布（其实就是遍历所有可能的移动方案），(x,y) 是一对横坐标， $\gamma(x,y)$ 比较“曲折”，以x为起始, y为目标，表明在 $\gamma$ 这个方案下要从 $p_r$ 的 x 位置拿多少数放到 y 位置上，从而让 $p_r$ 在 x或y 位置上与 $p_g$ 的 x或y 位置相同，有 $\sum_x \gamma(x,y)=p_g(y),\sum_y \gamma(x,y)=p_r(x)$ 。
对于某个方案 $\gamma$ ，EM距离为：

\sum_{(x,y)}\gamma(x,y)|x-y| = E_{(x,y)\sim\gamma}[|x-y|]

为什么Wasserstein距离更好#

前文提到，JS 散度的问题在于，当两个流形不相交的时候，无法给出平滑的结果，但Wasserstein距离可以。构造一个例子（流形P, Q）来解释这一现象：

\begin{aligned} \forall(x,y)\in P&, x=0 ,y\sim U(0,1) \\ \forall(x,y)\in Q&, x=\theta(0\le\theta\le1),y\sim U(0,1) \end{aligned}

这样当 $\theta\neq0$ 的时候，两个流形就完全不相交。在相交和不相交的情况下计算PQ的KL散度、JS散度、Wasserstein距离：
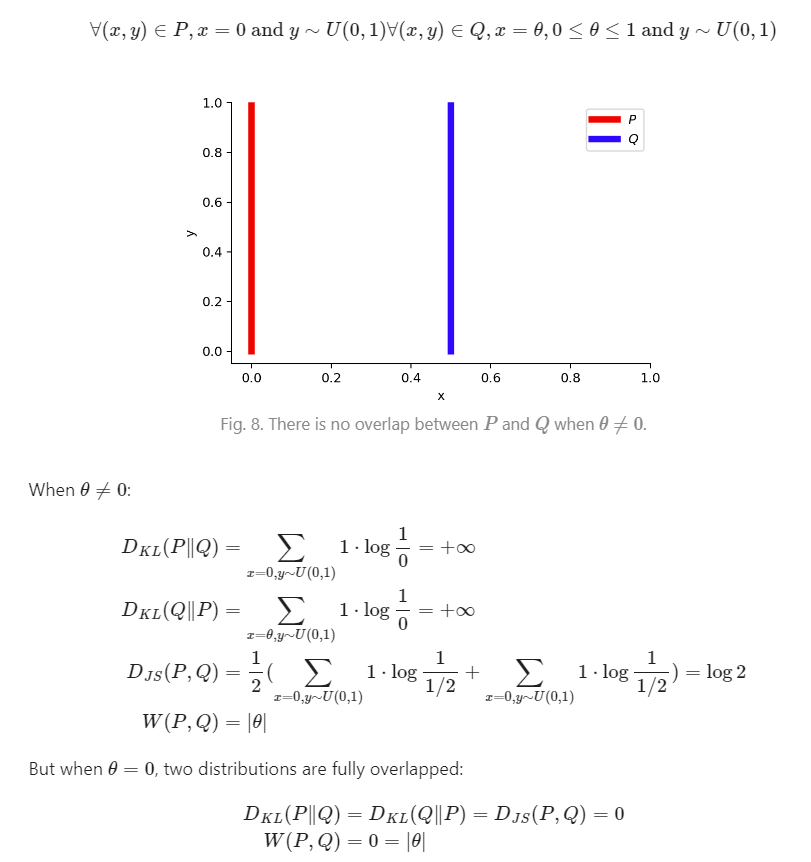
不相交的时候的KL,JS,Wa距离

可以看到，不相交的时候 KL 散度直接无穷，JS 散度发生了跳变（ $\theta$ 变为0的时候），而Wasserstein距离则是平滑的。

把Wasserstein距离用到GAN中#

Wasserstein本身是一个最优化问题，很难直接求解。用了Kantorovich-Rubinstein对偶条件将它进行转换（好像在什么地方看到过，这个对偶，最优化..? 这个转变比较复杂，关于这个K-R对偶和Wasserstein距离的变换，WengLilian推荐了一个awsome post，之后有兴趣可以看看）：

W(p_r,p_g)=\frac{1}{K}\sup_{||f||_L\le K} E_{x\sim p_r(x)}[f(x)]-E_{x\sim p_g(x)}[f(x)]

其中 $f$ 是一个函数，它需要满足 $|f|_L\le K$ ，也就是满足 K-Lipschitz continuous （K利普希茨连续，回去复习数分…Orz）。具体就是：

\forall x_1,x_2 \in R, |f(x_1)-f(x_2)|\le K|x_1-x_2|

但是注意，一个利普希茨连续的函数未必处处可微，比如 $f(x)=|x|$ 。

这个 $f$ 函数是学习出来的。在使用了 Wasserstein距离的 W-GAN 中，“辨别器”就是要学习这个 f 函数，记为 $\{f_w\}_{w\in W}$ ，这是一个派生自 K-利普希茨连续函数集合的函数，用参数 w 去控制，“辨别器”的优化目标就变成了：

L(p_r,p_g)=W(p_r,p_g)=\max_{w\in W} E_{x\sim p_r(x)}[f_w(x)]-E_{z\sim p_g(z)}[f_w(g_\theta(z))]

可以看出，WGAN 中的“辨别器”虽然仍叫辨别器，形式上很相似，但已经有了截然不同的数学身份了。

另一个问题是如何保证迭代过程中 $f_w$ 始终有 K-利普希茨连续性？方法很简单粗暴但也很有效，每次更新 $f_w$ 后都把参数 w 截断到一个小范围，比如 [-0.01, 0.01]，从而直接保证 $f_w$ 不会比原本“大太多”，维持利普希茨连续性。——当然，原作者自己也说这种方式很terrible。

G的优化目标也没什么变化：

\max_\theta E_{z\sim p_z(z)}[f_w(g_\theta(z))]

WGAN的伪代码为：
WGAN伪代码

然而，WGAN虽然理论上有比较精彩的推导，但仍然有不稳定、难收敛、梯度消失的问题…关于 w 的权重clip，后面更普遍用的是 gradient penalty。